в случае движения точки по абсолютно гладкой линии, т. е. при идеальной связи, в уравнениях движения (13.4), которые примут следующий вид:

проекции реакции связи N будут присутствовать только во втором и третьем уравнениях. Опять имеет место смешанная задача динамики точки, причем задачи разделяются - сначала из первого уравнения по заданным активным силам и начальным условиям определяют движение точки, а затем из второго и третьего уравнений находят реакцию связи.

В случае неидеальной связи появится третья составляющая реакции, проекция которой будет зависеть от физических условий взаимодействия точки со связью и войдет в первое уравнение. Задачи динамики могут не разделиться, так как уравнения окажутся связанными.

Пример 13.5. Материальная точка М начинает движение из положения, близкого к крайней верхней точке А сферического купола, радиус которого г,

Р = mg (рис. 13.4). Пренебрегая трением, определить, на какой высоте от плоскости основания нарушится контакт точки с поверхностью купола.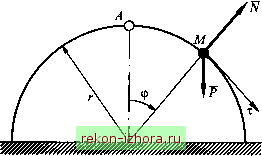

Рис. 13.4

Решение. В проекциях на естественные оси уравнения движения точки имеют вид

т-- = mgsirup; т - = mgcos<p - N . at г

Выполнив замену независимой переменной dvldt =vdv/(rd(p), приведем первое уравнение к виду

vdv = gr sin ((р

и после интегрирования при начальных условиях v = О при ф = фо получим

=2gr(cosфo~cosф),

где созфо ~ 1.

Данное выражение определяет зависимость скорости точки от угловой координаты только на участке ее движения в контакте с поверхностью купола. Из второго уравнения находим

N = mgcos<p-mv/r = mg(Зcosф-2).

Контакт нарушится в положении, где = О , т. е. при созф* = 2/3 . Высота

точки над основанием в этом положении Л = гсозф* = 2г/3.

Пример 13.6. Разгонный участок лыжного трамплина выполнен в виде дуги окружности радиусом г = 50м. Лыжник, масса которого т = 80кг, начинает

разгон без начальной скорости из точки старта Л, расположенной на высоте h = г/2 над точкой отрыва В (рис. 13.5). На лыжника действует сила сопротивления воздуха R = -iiv v {R = \iv), где ii = 0,16 Н с/м - аэродинамический коэффициент, сила трения о снег, коэффициент трения скольжения / = ОД и сила

тяжести Р =mg . Рассматривая лыжника как материальную точку, найти его скорость в конце участка разгона.

Решение. Определим положение лыжника на участке разгона естественной

координатой S = AM = гф (см. рис. 13.5). Рис. 13.5 Векторное дифференциальное уравнение

движения

dv - - - -т- = P-\-N -{-F--R

спроецируем соответственно на касательную и нормаль естественного трехгранника:

т- = mg sm а - - \iv ;

(13.10)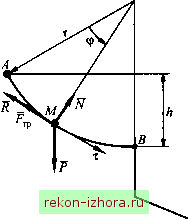

m - = -mg cosa + N, r

где а = 7с/3-ф .

Найдем из второго уравнения и подставим выражение F fN /(mgcosa + mvvo в первое уравнение (13.10). Получим нелинейное дифференциальное уравнение

т- = -(ц + /m/r)vj + mg(sina--/cosa). (13.11)

Выполним замену независимой переменной dvjdt = vd}>/{rd(p), введем новую переменную z = = и представим уравнение (13.11) в виде

- + 2/:z = M[sin(7i/3 - ф) - / cos(7c/3 - ф)], dip

где /: = (гц/m) + / = 0,2 - приведенный коэффициент трения; u = 2gr = = 980 м vc .

В частном решении

Z* =у48ш(7с/3-ф)+С08(71/3-ф)

этого линейного уравнения константы А и В, определенные методом неопределенных коэффициентов, равны

, 2k + f 2 о 1-2/ 2

А =-В =-=v

Постоянная интегрирования С общего решения

Z = С ехр(-2/:ф) + А sin(7c/3 - ф) + Всоз{п/3 - ф)

в соответствии с начальным условием (z = О при ф = О) равна

С = -sin(7i/3) - Всо8{п/3) = -0,787м.

Тогда в конечной точке В участка разгона при ф = тс/З скорость лыжника будет

Уд = ylB-hCQxp{-2kn/3) = м24/29-0,787ехр(-0,4189) = 0,5567м = 17,4 м/с .

Движение лыжника без учета сопротивления воздуха описывается более простым дифференциальным уравнением, которое можно получить из (13.11), положив в нем ц = О и / = О . Решение

Z = м [cos(7c/3 - ф) - С08(Я/3)]

этого уравнения при тех же начальных условиях позволяет найти другое значение скорости в конце участка разгона:

Vb = ylgrU - cos(7t/3)] = yl2 = 22,1 м/с,

которое показывает, что сопротивление воздуха заметно снижает скорость лыжника.