

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Теоретическая механика в соответствии с начальными для этапа падения условиями (= О при z-H) постоянная интефирования Сз = 1п(м2)-2ЯД. Таким образом, зависимость проекции скорости точки от координаты имеет у, = - 1-ехр[-2(Я-2)А], откуда скорость приземления точки = v,(0) = Uyl\-Qxp(-2H/X) = u-Qxpi-lG) = 0,894 = 43,8 м/с. Пример 13.3. Материальная точка массой т, находящаяся на некоторой высоте над поверхностью Земли, движется в условиях ветра, дующего равномерно со скоростью и. Сила сопротивления, действующая на точку со стороны воздуха, R = -\xv, где ц = const > О, v, - скорость точки относительно воздуха. Точка начинает движение с начальной абсолютной скоростью vq направленной горизонтально под прямым углом к скорости ветра. Решение. Совместим начало системы отсчета с исходным положением точки, а связанные с Землей оси направим как показано на рис. 13.2. Векторное уравнение движения точки dv - - = Р + R = mg-\x{v -и) 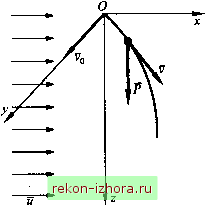 Рис. 13.2 в проекциях на координатные оси имеет вид тх+цх = [iu; ту+ \ху = 0; mz+ \iz = mg . Разделив эти уравнения на ц и обозначив т = т/\х, где т - постоянная времени, получим тх + х = и; ту + у = 0; xz-\-z = gx. Как видно, движение точки описывается системой несвязанных линейных дифференциальных уравнений, общее решение которой л: = + С, + Cj ехр(- т); , 3/ = Сз + С4ехр(- т); z = gT/ + C5 + Qexp(- T). Определив с помощью начальных условий: (0) = у{0) = z(0) = О, л:(0) = О, т = vo, z(0>= О , произвольные постоянные интефирования, приведем кинематические уравнения движения точки к виду X = и/ - ит[\ - ехр(-г/т)]; 3/ = УоТ[1-ехр(~ т)]; Проекции скорости точки изменяются по закону v,=w[l-expHA)]; v. =Уоехр(- т); V, =gT[l-exp(- T)]. Из этих уравнений следует, что при / -> оо Vj, -> м , -> О, -> gr, т. е. со временем точка будет двигаться практически в вертикальной плоскости с установившейся скоростью V = ui + gxk . 13.4. Движение несвободной материальной точки В рассмотренных выше задачах движение материальной точки определялось начальными условиями и взаимодействием ее с силовыми полями и окружающей средой. Все силы, приложенные к точке, выступали как заданные, т. е. как известные функции г, г и V . Взаимодействие с другими телами путем прямого контакта и связанные с этим взаимодействием какие-либо ограничения на движение в пространстве отсутствовали. Если на движение материальной точки в пространстве не налагаются ограничения, то она называется свободной. Однако чаще движение материальной точки сопровождается непосредственным взаимодействием ее с другими материальными телами. Аналогично схематизации свойств материальных тел это взаимодействие также схематизируется в виде кинематических ограничений, налагаемых на движение. В такой ситуации точку называют несвободной, а условия, стесняющие свободу ее движения, - связями. Связь, выраженная уравнением f{x,y,z) = Q, (13.6) является геометрической и означает, что точка движется по некоторой неизменной (время / в уравнение связи явно не входит) по- верхности и не может ее покинуть ни в какую сторону. Геометрическая связь такого типа называется стационарной и неосво-бождающей. Освобождающие связи выражаются неравенствами. В случае движения по поверхности число степеней свободы материальной точки, определяемое числом независимых координат, необходимых для однозначного задания положения, меньше, чем у свободной точки, и равняется двум. Еще меньшим будет число степеней свободы, если на точку наложены две связи. Это означает, что при движении точка должна все время оставаться на линии пересечения поверхностей обеих связей. Так как в соответствии с аксиомой о связях последние могут быть отброшены, а их действие заменено соответствующими силами, уравнение динамики несвободной материальной точки примет вид m - = F + R. (13.7) Здесь к активным силам, равнодействующая которых F , добавляется динамическая реакция связи R . Реакция R является пассивной силой, так как зависит от приложенных к точке активных сил, физических свойств связи и движения точки. Последнее определяет ее отличие от реакции связи в статике, что подчеркивается ее названием. Реакцию связи R можно всегда разложить по двум направлениям на составляющие, одну из которых N направить по нормали к поверхности связи, определяемой (13.6), а другую - в плоскости, перпендикулярной к нормали. Если второй составляющей пренебречь, то поверхность можно считать абсолютно гладкой, а связь - идеальной. В этом случае реакцию связи представляют в виде = A.grad(/), где Х = N/gmd(f) - скалярный коэффициент, называемый множителем связи. Векторное уравнение движения несвободной точки с идеальной связью принимает вид dv m- = F + Xgrad(f). at В проекциях на оси декартовой системы координат получаем уравнения
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |