в формуле (В.71) проекции одного и того же вектора b на оси соответствующих систем координат считаются элементами векторов-массивов В и b а скалярные произведения двух ортов - элементами матрицы А, т.е. ay=i-i, аз = у / ит. д.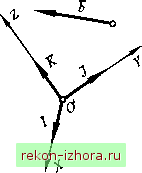

Рис. В.17

Отметим ряд важных свойств формулы (В.71) и матрицы А, причем условимся называть систему координат с ортами /, у,

к - первой, а с ортами I, J, К - второй.

1. Формула (В.71) определяет правила расчета проекций вектора на оси второй системы координат по его известным проекциям на оси первой системы, при этом матрица А считается матрицей перехода от осей первой системы координат к осям второй.

2. Согласно формуле (В.28), скалярные произведения соответствующих ортов разноименных осей координат равны косинусам углов между перемножаемыми ортами (или между соответ-

ствующими осями систем координат), т. е. = / 7 = cos(a; , X),

л

а= j I - Qos{y ,Х) ит. д. Поэтому матрицу А называют матрицей направляющих косинусов.

3. Элементы каждой строки матрицы являются проекциями соответствующего орта второй системы координат на оси первой, а элементы каждого столбца матрицы - проекциями соответствующего орта первой системы координат на оси второй, например:

7 = (а1 а,2,а,з); а =/; ; =/.

/ =(а ,а2 аз1) ; а =/;; а аз, =/г.

4. Сумма квадратов элементов каждой строки или каждого столбца равна единице, так как такая сумма выражает квадрат модуля орта, например:

5. Скалярное произведение двух различных строк или двух различных столбцов равно нулю, так как такое произведение соответствует скалярному произведению двух ортогональных векторов, например:

6. Определитель матрицы равен единице:

detA = l.

Этот результат можно получить, опираясь на формулу расчета смешанного произведения трех векторов (/, у, к или / , J, К\ образующих правую тройку. Он соответствует объему куба со стороной, равной единице.

7. Обратная матрица А равна матрице, транспонированной к матрице А:

А-=А\

8. Формула обратного пересчета проекций вектора на оси первой системы координат по его известным проекциям на оси второй имеет вид

ЬкВ. (В.72)

В.8. Вектор-функция. Годограф вектора. Дифференцирование вектора по скалярному аргументу

Если модуль и направление вектора А зависят от значений, принимаемых переменными /, w, v, w, то вектор А называется векторной функцией этих переменных, или вектор-функцией.

Ограничимся рассмотрением вектор-функций только от одной независимой переменной

A=A(t). (В.73)

При этом в общем случае с изменением скаляра / непрерывно изменяются и модуль, и направление вектора А . Следовательно, с учетом (В.1) можно записать

A=A(i)a,(i) = A(t), (В.74)

В частных случаях вектор А может изменяться или только по модулю:

ао = const, А = A(t)aQ, (В.75)

или только по направлению:

>4 = const, А=Аа(0. (В.76)

Если вектор А =A(t) = OM в процессе его изменения всегда откладывается от общего начала (полюса) О (рис. В. 18, а), то геометрическим местом концов этого вектора будет некоторая кривая (плоская или пространственная), называемая годографом вектора А .

Если полюс О принять за начало прямоугольной системы координат, то, согласно (В.7),

A=A,(t)i-Ay{t)j + Ait)k, (В.77)

где А{(), /1Д/), A(t) - проекции вектора А на оси координат. Тогда уравнения годографа вектора А, записанные в параметрической форме, имеют вид

х = Л(0, У = Ау{0, z = A{t). (В.78)

В частности, если вектор А изменяется только по модулю (см. (В.75)), его годографом будет прямая, вдоль которой направ-