

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Теоретическая механика мер автомобиля, которому ведущее колесо стремится сообщить движение вправо. Из условия равновесия колеса получаем В предельном состоянии равновесия Ведущее колесо может сообщать автомобилю силу только тогда, когда к колесу будет приложен момент Л/ этрм случае полностью используется максимальная сила трения скольжения F, 3 =/Л. При Л/<Мзх сила <шах. при М>М, сила Q должна быть больше F, что невозможно (колесо начинает буксовать); ведущее колесо может сообщать автомобилю силу, не превышающую силу трения сколь- шЙш жения. Такую силу называют силой тяги по сцеплению. Рис. 10.6 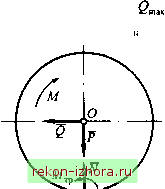 Трение нити о цилиндрическую поверхность (задача Эйлера) Пусть круглый вал обмотан нитью, к одному концу которой приложена сила F, (рис. 10.7). Определим наименьшую силу которую надо приложить к другому концу нити, чтобы удержать силу F если угол охвата нити у, а коэффициент трения нити о вал/ Рассмотрим равновесие элементарного участка нити DE длиной ds = rd, где г - радиус вала. В точках D иЕ натяжение нити будет соответственно Г и {Т + dT). На нить, кроме того, действует сила нормального давления вала dN и сила трения dF, приложенные в точке С. Сумма проекций всех сил на касательную к валу в точке С равна нулю. Тогда dTdF.  Рис. 10.7 Наименьшее значение силы F2 будет соответствовать предельному случаю равновесия, поэтому df = fdN. Проецируя все силы на нормаль Су, находим dN = (T + T + dT)sm(d/2) = 2Г(ф/2) = . Подставим это значение dN в выражение dT = fdN: dT = fTd. Разделим переменные и проинтегрируем полученное уравнение в пределах от F2 до F, и от О до у: Отсюда находим При / = О, как и следовало ожидать, = F,. Увеличивая угол охвата у, можно значительно уменьшить силу . Например, при / = 0,5 и у = 4я F2 =0,002Fi. Рассмотренная задача часто встречается в практике, например при расчете Ленточных тормозов или швартовки кораблей к причалу. Пример 10,1. Цилиндрический каток весом Р, обмотанный двумя симметрично расположенными нитями, находится на наклонной плоскости, образующей угол а с горизонтом (рис. 10.8, а). Найти, при каких значениях угла а каток будет в равновесии, если коэффициент трения скольжения между катком и плоскостью равен/ Трением качения пренебречь. 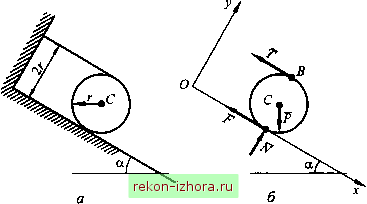 Рис. 10.8 Решение, Освободим каток от связей, заменив их реакциями (рис. 10.8, б). При равновесии катка на плоскости Ma(FJ = Prsina - F 2r = О . В предельном случае равновесия F = F = JN , где N = Pcosa p. Следовательно, sina p =2/cosa p. Равновесие катка возможно, если а < а где ttnp =arctg2/. Пример 10,2, Грузозахватный механизм (рис. 10.9, а) состоит из двух одинаковых рычагов У и 2, конуса 3 и стяжки 4. Определить значение коэффициентов трения скольжения между пластинами механизма и грузом 5, при которых
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |