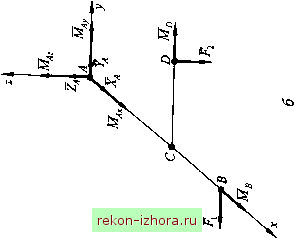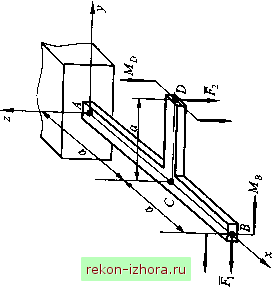(9.3)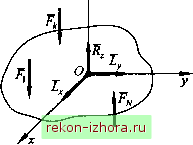

Рис. 9.2

Условия равновесия плоской системы сил

Для плоской системы сил условия равновесия будут частным случаем уравнений (9.2), определяющих условия равновесия пространственной системы сил. Например, если силы расположены в плоскости Оху, то аналитические условия равновесия можно записать в виде

=1*, =0; R, =1 =0; Lo =tMo(F,) = 0. (9.4)

Л=1 к=\ к=\

Для равновесш произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма алгебраических моментов этих сил относительно любого центра О были равны нулю.

Алгебраическим моментом силы относительно точки называют момент силы относительно оси, проходящей через данную точку перпендикулярно плоскости, в которой расположена сила и точка (см. (8.11)).

Вместо (9.2) иногда удобно применить условия равновесия в виде уравнений трех моментов: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы

алгебраических моментов всех этих сил относительно любых трех центров А, Д С, не лежащих на одной прямой, были равны нулю:

fM,(F,) = 0; f,M,(F,) = 0; fM (F,) = 0. (9.5)

ы\ k=\ ы\

Необходимость утверждения следует из того, что третье условие (9.4) справедливо для любой точки. Достаточность докажем методом от противного, используя теорему о приведении произвольной системы сил к центру. Допустим, что плоская система сил не находится в равновесии. Тогда, приводя ее поочередно к точкам А, В, С, будем иметь в этих точках равнодействующую R *. Для выполнения равенств (9.5) равнодействующая должна пройти одновременно через все три точки, а это невозможно, так как точки не лежат на одной прямой. Следовательно, равнодействующая равна нулю и система сил, удовлетворяющая равенствам (9.5), находится в равновесии.

Пример 9,2. Составить условия равновесия для плоской системы сил, приложенных к балке (рис. 9.3).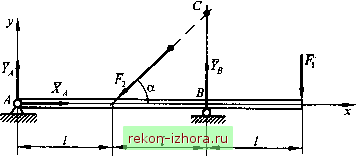

Рис. 9.3

Решение. На основании уравнений (9.4) имеем

lA = JLM) = -i/sina + Y,2l-F,y = О, или, согласно уравнениям (9.5),