

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Теоретическая механика Сравнивая между собой полученные выражения для М, получаем математическую запись теоремы Вариньона Проецируя векторы, входящие в обе части этого равенства, на любую ось, проходящую через центр О, находим, что теорема Вариньона справедлива и для моментов относительно оси. Реакция заделки Связь, которая запрещает как линейные, так и угловые перемещения твердого тела, называется заделкой. При приведении сил реакции заделки к точке А (рис. 8.35) на основании теоремы о приведении системы сил к заданному центру получим силу и пару сил с моментом . Модуль силы и момент пары сил в заделке могут быть определены из условий равновесия твердого тела, к которому они приложены. Например, для балки, показанной на рис. 8.35 (плоская система сил), будем иметь R,=F,M,=Fl. 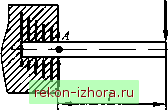 Рис. 8.35 Соотношение между главными моментами системы сил относительно двух центров приведения Допустим, что при приведении системы сил к центру о получили главный вектор r и главный момент Lq . Найдем выражение главного момента Lq той же системы сил относительно нового центра О, (рис. 8.36) 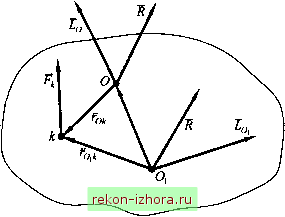 Рис. 8.36 Из векторного треугольника ОкО находим Тогда Lo, =1,(0,0 +г ,)xF, =0,OxF, xF,), Окончательно получаем Lf) =L() +0,OxR, (8.19) Таким образом, главный момент системы сил относительно второго центра приведения О, равен сумме главного момента системы сш относительно первого центра приведения О и векторного момента главного вектора, пршоженного в первом центре приведения, относительно второго. Инварианты системы сил Инвариантами системы сил называются скалярные или векторные величины, не зависящие от выбора центра приведения. Первый инвариант - главный вектор системы сил. Для лю-
бого центра приведения R=YF, . Второй инвариант - скалярное произведение главного вектора на главный момент системы сил. Для доказательства этого утверждения умножим равенство (8.19) скалярно на главный вектор R : LoR=LoR+ (OjOX R)R . Поскольку {OOxR) R = О,то LqRLqR , Частные случаи приведения пространственной системы сил к простейшему виду Покажем, к какому простейшему виду можно привести пространственную систему сил, не находящихся в равновесии. В общем случае любая система сил эквивалентна силе, равной главному вектору R, и паре сил, момент М которой равен главному моменту Lq относительно центра приведения О: R-fFr, M = f(Fo,xF,) = fM iF,)Lo. к=\ к=\ к=] Частные случаи дальнейшего упрощения можно получить из анализа второго инварианта системы сил. Допустим, что второй инвариант системы сил LqR=0,тогда возможны следующие случаи. 1. Если для данной системы сил 1 = О, а RO,to система сил приводится к равнодействующей R *, равной R и проходящей через точку О, 2. Если i? =0, а L() 0, то система сил приводится к паре сил с моментом М = 1, который на основании (8.19) не зависит от выбора центра О. 3. Если RO, Lq 0, ио Lq ±R, то заданная система сил приводится к равнодействующей R *, равной R , но проходящей не через точку О, а через точку , отстоящую от точки О на расстоянии
|
||||||||
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |