Решение. Рассмотрим равновесие стержня. Реакцию связи неподвижного шарнира вместо двух составляющих представим одной силой , направленной в точку D пересечения линий действия сил Р и Rg (рис. 8.16, б). Из геометрических соображений (см. рис. 8.16, а, б) находим Р, = 60° и pj = 30°, а из силового треугольника (рис. 8.16, в) определяем

R,=P

Rb=P

8.4. Момент силы относительно точки и относительно оси

Момент силы относительно точки

Пусть к телу в точке А приложена сила F (рис. 8.17). Тогда моментом силы F относительно точки О называется вектор M(){F), приложенный в точке О перпендикулярно плоскости треугольника ОАВ и равный

Mo{F) = rxF, (8.7)

где г - радиус-вектор, проведенный из точки О в точку А приложения силы F .

I MoiF)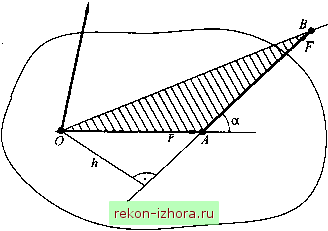

Модуль вектора Mq(F) равен произведению модуля силы

F на расстояние h от точки О до линии действия силы, которое называется плечом силы относительно точки О, т. е.

Mo{F)\ = \F\-\r\sma = Fh,

Нетрудно заметить, что радиус-вектор г из точки О может быть проведен не только в точку А, но и в любую другую точку, лежащую на линии действия силы F , так как при этом будет изменяться и г, и угол а, однако rsina = A останется без изменения.

Момент силы относительно точки равен нулю, когда линия действия силы проходит через эту точку.

Момент системы сил относительно точки

Если мы имеем систему сил , ,..., ,..., (рис. 8.18), то вектор Lq , равный сумме моментов всех этих сил относительно точки О

(8.8)

называется главным моментом системы сил относительно точки О.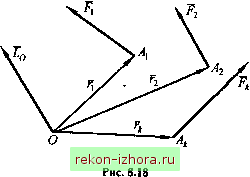

Если все силы приложены в одной точке (рис. 8.19), то

Lo=f(rxF,) = rxfF,=rxR\ (8.9)

Вьфажение (8.9) представляет собой векторную запись теоремы Вариньона: момент равнодействующей относительно какой-либо точки равен сумме моментов составляющих сш относительно той же точки.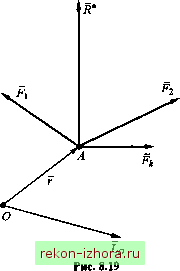

Момент силы относительно оси

Моментом силыР относительно оси называется проекция векторного момента этой силы, взятого относительно любой точки оси, на эту ось, т. е.

M,(F) = (FxF),. (8.10)

Покажем, что проекция момента силы F , взятого относительно какой-либо точки О оси Oz, на эту ось не зависит от положения точки на оси (рис. 8.20).

Равенство (8.10) можно представить в виде

MF) = (r xF), =(r xF)Jfc =(jfc xr)F.

Из рис. 8.20 следует, что модуль векторного произведения (кхг) есть величина постоянная для любой точки на оси. Численно он равен удвоенной площади треугольника с основанием к и высо-