На рис. 8.9 и 8.10 показаны реакции связей соответственно для стержня АВ, опирающегося в точке А на гладкую стену и подвешенного в точке В к стене нитью, и полукруглой плоской арки, опирающейся в точке А на подвижный шарнир (каток), а в точке В - на неподвижный шарнир.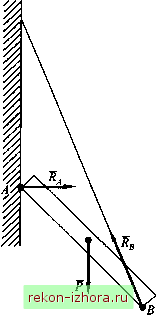

Рис. 8.9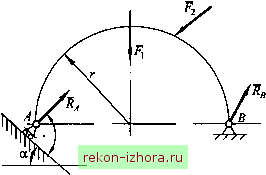

8.3. Система сходящихся сил Равнодействующая системы сходящихся сил

Систему сил, приложенных к твердому телу, называют системой сходящихся сил, если линии действия всех сил пересекаются в одной точке.

Пусть на тело действуют силы, линии действия которых расположены в пространстве и пересекаются в одной точке О (рис. 8.11, а). Перенеся силы вдоль линий действия в эту точку и сложив их последовательно по правилу параллелограмма, найдем

равнодействуюыую R* данной системы сил (рис. 8.11, б):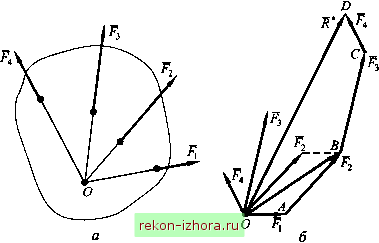

Рис. 8.11

В общем случае для системы сходящихся сил:

(8.1)

Результат сложения векторов не зависит от последовательности их сложения. Графическое сложение векторов возможно и без построения параллелограммов сил. Для этого нужно

от конца вектора одной силы отложить вектор другой силы, затем от его конца отложить вектор какой-либо третьей силы и т. д., пока не будут отложены все силы. Для нахождения равнодействующей системы сил нужно соединить начало первого вектора с концом последнего (см. рис. 8.11, б). Многоугольник OABCD называется силовым многоугольником.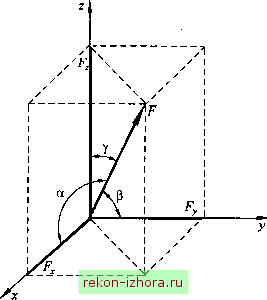

Рис. 8.12

Таким образом, система сходящихся сил эквивалентна одной равнодействующей сше, которую можно определить замыкаю-

щим вектором R* сшового многоугольника, построенного на векторах-силах системы сходящихся сил. Другими словами, равнодействующая системы сходящихся сил равна их геометрической сумме.

Аналитический способ задания и сложения сил

Аналитический способ решения задач статики основывается на представлении вектора силы в виде трех его составляющих по