Используя соотношения (В. 19) и (В.23), запишем скалярное произведение двух векторов через их проекции. Если А =AJ + Ayj + A,k, В =Bj + By]+ B,k,то

AB=(Aj + Ayj + A,k)(Bj + By] + bJc) =

(B-24)

= 5cos( , 5) = AB +AyBy+ A,B,.

Таким образом, скалярное произведение двух векторов равно сумме попарных произведений одноименных (по индексу) проекций векторов на координатные оси.

Из (В.24) имеем выражение для косинуса угла между векторами А и В :

- А В + АВ + А,В,

cos(A , 5) = = ---~. (В.25)

А В А В

Если 15 ,то

А,В-АуВу+АВ=0. (В.26)

Рассматривая выражение (В.2), видим, что

4=cos(,/) = l.cos( ,/) = /о, (В.27) где /о - единичный вектор оси /.

Из (В.25) следует, что косинус угла между единичными векторами Qq и *о равен скалярному произведению этих векторов:

cos(ao?6o) = o-*o- (В.28) Векторным произведением двух векторов Ах В называется вектор, модуль которого равен произведению модулей перемножаемых векторов на синус угла между ними, а направление перпендикулярно плоскости, проходящей через эти векторы (рис. В.11, а), и выбрано так, чтобы с конца полученного вектора, можно видеть, что для кратчайшего совмещения первого сомножителя со вторым его нужно вращать против хода часовой стрелки. Согласно определению, если

1х5=С, (В.29)

с =C = 5sin(I,5)=mi.OOZ)£F, (В.ЗО)

т. е. модуль векторного произведения численно равен площади параллелограмма ODEF, построенного на перемножаемых векторах.

С=АхВ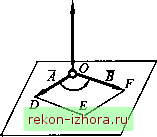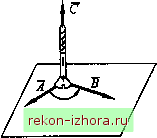

Рис. В.11

По установленному соглашению направление векторного произведения С определяется правилом правого винта (рис. В.11, б). В соответствии с этим правилом в правой системе прямоугольных декартовых координат (рис. В.12) направление кратчайшего совмещения оси Ох с осью Оу видно с конца оси Oz против направления движения часовой стрелки. Единичные векторы i, j\ к образуют правую систему единичных векторов.

В дальнейшем будем пользоваться именно правой системой координат, чтобы иметь единообразный подход к рассмотрению вопросов теории и к решению задач.

Векторное произведение двух векторов свойством переместительности не обладает (рис. В.13):

АхВ=ВхА). (В.31)

При умножении вектора на скаляр векторное произведение обладает свойством сочетательности:

(тА)хВ= тп(А xВ). (В.32)

По отношению к сложению векторов векторное произведение обладает свойством распределительности:

(А + В)хСАхС+ВхС . (В.ЗЗ)

Отметим частные случаи векторного умножения:

если

если ALB, то sm{A ,В) = \, Ах В

= АВ.

(В.34) (В.35)

(В.36)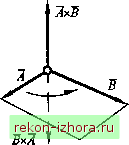

Рис. В.12

Рис. В.13

Для единичных векторов i, j и к (см. рис. В.12) формулы (В J5) и (В.36) дают

IxJ = jx] = kxk = 0; (В.37)

/ X j = k , jxk=i, kxi =j. (B.38)

Запишем теперь выражение векторного произведения через его проекции на координатные оси. Имеем: А = А J + Ayj + Ak,

В = BJ + Byj + В,к . Перемножая правые части этих соотношений векторно и пользуясь последовательно выражениями (В.ЗЗ), (В.37) и (В.38), получаем

АхВ=(АуВ,-А,Ву)1 + (А,В,-А,В,)] + {А,Ву-АуВ,)к, (В.39) или

АхВ =

В. 5

(В.40)

Из (В.40) видно, что проекции на оси координат для векторного произведения равны