

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Теоретическая механика Таким образом, искомые проекции вектора угловой скорости на оси подвижной (скрепленной с телом) системы координат будут равны (Ох =vi/sin6sin9 + 6cos9; щ =vi/sin6cos9-6sin9; (4.8) (Oz =х/со89 + ф. Полученные соотношения носят название кинематических уравнений Эйлера, Они устанавливают связь между проекциями вектора угловой скорости тела с5, углами Эйлера \/, 0, ф и их первыми производными по времени. Подстановка (4.8) в (4.7) и дает искомые проекции вектора V на оси координат OXYZ. Скорости точек тела, лежащих на мгновенной оси (см. рис. 4.9), в рассматриваемый момент времени равны нулю, и их проекции на оси координат должны удовлетворять следующим уравнениям: (OyZ -(oY = 0; (оХ -(OxZ = 0; (oY-(ОуХ-О, 2 (4.9) (Ох (Оу (Oz Соотношения (4.9) являются уравнениями прямых, проходящих через начало координат, и представляют собой уравнения мгновенных осей вращения тела в подвижной системе координат. Если величины, входящие в (4.9), рассматривать как функции времени, то эти соотношения будут представлять собой параметрическую ощ уравнений подвижного аксоида. Для неподвижной системы координат Oxyz в формулы (4.7) и (4.9) вместо (О;, (Оу, (о и X, 7, Z нужно подставить (о, (Оу, со и х, у, Z, т. е. проекции угловой скорости с5 и радиус-вектора г точки тела на неподвижные оси Ох, Оу, Oz. Если положение мгновенной оси вращения установлено, то для определения модуля угловой скорости тела со в данный момент времени достаточно модуль скорости какой-либо точки тела в тот же момент времени разделить на кратчайшее расстояние от нее до мгновенной оси вращения тела. Пример 4.L Найти неподвижный и подвижный аксоиды и угЛовую скорость кон>са высотой Н и углом полураствора при вершине а (рис. 4.11), если кон\ с катится по горизонтальной неподвижной плоскости без скольжения, его вершина О неподвижна, а скорость v центра С его основания постоянна. 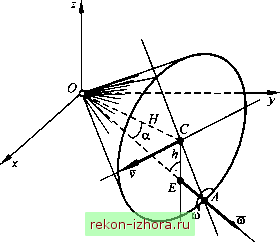 Рис. 4.11 Решение. Так как движение конуса происходит без скольжения, то скорость его точки А контакта с неподвижным основанием равна нулю. Неподвижной точкой является и точка О. Следовательно, прямая OA - мгновенная ось вращения конуса. Геометрическое место мгновенных осей вращения в неподвижной системе координат Oxyz - плоскость Оху, по которой катится конус (неподвижный аксоид). В подвижной же системе, связанной с конусом, геометрическое место мгновенных осей образует коническую поверхность, совпадающую с поверхностью самого конуса (подвижный аксоид). Так как v = юЛ, а h - СЕ = Hsina , то 0) = Я sin а Если вектор скорости точки С конуса направлен в сторону, указанную на рис. 4.11, то вектор его мгновенной угловой скорости направлен от вершины конуса к основанию по мгновенной оси вращения OA, Учитывая, что скорость какой-либо точки тела, с одной стороны, есть первая производная по времени от ее радиус-вектора г , проведенного из неподвижной точки тела, а с другой - определяется векторной формулой Эйлера (4.9), можно записать - = сохг. (4.10) Поскольку модуль радиус-вектора г - расстояние между двумя точками М w О твердого тела - постоянен (см. рис. 4.9), равенство (4.10) можно рассматривать как формулу для вычисления производной по времени от вектора постоянного модуля, изменение которого сводится лишь к его повороту вокруг неподвижной точки. Если взять в качестве таких векторов единичные векторы 7, J, АГ подвижной системы координат OXYZ, вращающейся с угловой скоростью со (см. рис. 4.9), то - = сох7; = coxJ; = сохАГ. (4.11) dt dt dt Формулы (4.11) называют формулами Пуассона. 4.6. Ускорения точек тела Рассмотрим твердое тело, вращающееся вокруг неподвижной точки О, и выберем в нем какую-либо точку Л/(рис. 4.12). Если в данный момент времени скорость точки тела равна v , то ее ускорение может быть выражено формулой a=dvldt. Полагая v = ю х г , запишем dv d (ico dr а = - = -(сохг) =-хг + сох - . dt dt dt dt Поскольку d/dt = г, й d r/dt = v = ш x г , то a = 8xr + wxv. (4.12) Установленное соотношение называют формулой Ривальса. Она дает представление о распределении ускорений точек в твердом теле, движущемся вокруг неподвижной точки. Ускорение а есть сумма двух ускорений. Первое азр=8хг (4.13) называют вращательным ускорением, второе
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |