

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Теоретическая механика В.З. Координаты вектора. Аналитическое задание вектора. Радиус-вектор точки Вектор А = ОМ (рис. В.5) считается заданным, если известны его модуль А и направление, т. е. направляющие косинусы углов а, Р и у, образуемых этой прямой с осями прямоугольной системы координат Oxyz: cos а = cos(jc, ОМ), cos р = cos(>, ОМ), cosy = cos(z,OM). (В.З)
Рис. в.5 Поскольку косинусы углов а, Р и у связаны между собой известным соотношением cos а + cos р + cos у = 1, то вектор однозначно определяется тремя независимыми величинами, называемыми координатами вектора. Удобнее всего принять за координаты вектора его проекции на оси декартовой прямоугольной системы координат: А =cosa; Ay =cosP; A =cosy. (B.4) Поскольку A.jg f* f* - j4. у TO модуль вектора и направляющие косинусы, согласно выражениям (В.З, В.4), определяются так: А = а1+а1+А, ; (В.5) cosa=- cosp = - А С08у=- (В.6) А Введем в рассмотрение единичные векторы (или орты) координатных осей. Обозначим их соответственно /, ]\ к (см. рис. В.5). Тогда А =AJ=iA cos а, Ay = Aj Acos, A = = Ak = к Acosy- ортогональные составляющие вектора A , поэтому АА+Ау+А =АтAyJАк . (В.7) Однако, согласно (В.1), А=Аа, aQ=A/A, Тогда Оо, = = ao/=/cosa, =aQy] = J cos, ISq =aQk :=k cosy. Следовательно, Uq = cos a, Qoy = cos p, = cos y, (B.8) т.е. проекции единичного вектора Oq на оси коорди- z нат равны косинусам углов а, Р, Y для вектора В частном случае, если вектор ОМ измеряется в линейных единицах и имеет свое начало в начале координат О, а конец - в некоторой точке М, он называется радиус-вектором точки М Тогда проекциями вектора ОМ = г (рис. В.6) являются координатых,уиг точки А/, и выражение для радиус-вектсфа точки А/имеет вид r=xJ + yj + zk, (В.9) 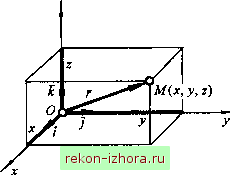 Рис. в.6 B.4. Сложение и вычитание векторов Суммой двух векторов А и В называется вектор А+В, соединяющий начало вектора А с концом вектора В (рис. В. 7, а, б), если вектор В отложен от конца вектора А . Это построение называется законом сложения векторов. Из рис. В.7, в ясно, что А+ВВ+А. (В.Ю)  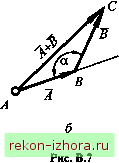 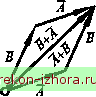 Таким образом, заключаем, что сложение двух векторов обладает свойством коммутативности (переместительности). Из А ABC (см. рис. В.7, б) имеем л но а = я - (, 5), тогда = А +В -lABcosa, А+в у1а+в+: -2ABcos(A, В). (В.11) Сумму нескольких векторов получим последовательным применением закона сложения двух векторов: сумму двух (>4 + 2) сложим с третьим вектором А (рис. В.8), полученную сумму (Ai+A2+A) сложим с четвертым вектором и т. д. Сложив сумму п -1 первых векторов (А ¥ А2 ++ Л-i) последним вектором А , получим сумму п векторов:
|
|||||||||||||||||||
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |