Глава 22 ОСНОВЫ НЕБЕСНОЙ МЕХАНИКИ

Небесная механика изучает движение искусственных и естественных небесных тел под действием сил, определяемых законом всемирного тяготения Ньютона, сил светового давления, сопротивления среды и др.

Классическими задачами небесной механики являются задача о движении материальной точки под действием центральной силы, задача двух тел, в которой рассматривается движение двух материальных точек в пространстве под действием сил взаимного притяжения, а также задачи трех и п тел.

22.1. Формулы Бине

Сила, линия действия которой проходит через неподвижную точку, называется центральной. Такая сила может быть как притягивающей, так и отталкивающей.

Рассмотрим движение материальной точки М, имеющей массу т, под действием силы F , линия действия которой все время проходит через неподвижную точку О, принимаемую за начало координат. В § 15.5 было доказано, что в задаче о движении точки под действием центральной силы существует интеграл площадей

К=г xmv =С (С = const), а траекторией точки М будет кривая, расположенная в неподвижной плоскости, перпендикулярной вектору С и проходящей через центр О центральной силы (случай С = О исключим из рассмотрения). В небесной механике эту плоскость называют плоскостью Лапласа.

Для описания движения точки М введем полярные координаты. Поместим полюс в неподвижный центр О и проведем полярную полуось через начальное положение точки (рис. 22.1). Уравнения движения точки в проекциях на оси полярной системы координат примут вид

т{г -rф) = F,; i)

т(2гф + гф) = 0.

Начальные условия таковы:

л . . Vq sin а

при Г = 0 r = R, ф = 0, r = vocosa, ф = --,

где а - угол между вектором Vq и полярной полуосью.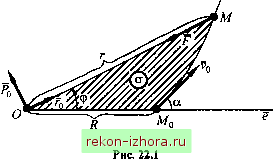

Из второго уравнения (22.1) следует

r2ф = C = const, (22.2)

т. е. под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью

а = гф/2 = С/2

так, что радиус-вектор точки за равные промежутки времени заметает равные площади. Эта закономерность имеет место при движении планет и выражает собой закон площадей Кеплера.

Первое уравнение (22.1) с учетом (22.2) можно представить в

виде

m = F+mC4r . (22.3)

Если F,. не зависит от ф, т.е. =F(r), уравнения движения точки решают последовательно: сначала из (22.3) определяют закон изменения во времени полярного радиуса г = r{t), а затем из (22.2) - зависимость ф = ф(/). Если же F, =(г,ф), уравнения будут связанными и их решают совместно.

Выведем такое дифференциальное уравнение, из решения которого можно сразу определить траекторию. Заменим дифференцирование по t дифференцированием по ф, учитывая существование интеграла площадей (22.2):

dt dt d(f>

d(p dr

d-r d(pdv,. С d

dt- dt d( r- Ф

C dr r d(?

dm Ф

= -C

d(\/r)

С d\l/r)

Тогда получим первую формулу Бине

(22.4)

(22.5)

(22.6)

позволяющую находить скорость в различных точках орбиты, если известны траектория г = г((р) и постоянная С секторной

скорости.

Подставив выражение (22.5) в (22.3), получим вторую формулу Бине

d\\lr) 1 d<p г

(22.7)

Формулы Бине позволяют находить решения как прямой, так и обратной задач динамики, т. е. определять центральную силу, если известна траектория движения точки, или определять траекторию, зная центральную силу. Если F явно не зависит от времени, для решения достаточно одного уравнения (22.7), представляющего собой дифференциальное уравнение траектории