

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Теоретическая механика Пример L5, В задаче, решаемой в примере 1.4, перейти от естественного способа задания движения точки М к заданию ее движения в декартовой системе координат Оху (см. рис. 1.12). Рассмотреть также движение точки в полярной системе координат, полярная ось которой совпадает с осью Ох декартовой системы координат. Записать уравнения траектории точки М в этих системах координат. Решение. Согласно чертежу, приведенному на рис. 1.12, геометрические соотношения для декартовых координат точки М имеют вид л = /? + /?со8а; y = Rs\na. Уравнения движения точки в декартовой системе координат, с учетом (1.56), можно записать так: x = R-\-Rcos[s(t)/R]; y = Rsin[s{t)/R], где закон движения точки по траектории s(t) имеет вид, приведенный в условии задачи из примера 1.4. Уравнение траектории в данном случае можно получить в форме При этом следует учесть диапазоны изменения декартовых координат точки: R<x<2R; -R<y<R. На рис. 1.12 видно, что полярный угол ф = а/2, а полярная координата г равна длине отрезка ОМ, являющегося стороной равнобедренного треугольника 00]М . Из этого треугольника находим ОМ = 2/?со8ф . Таким образом, уравнения движения точки М в полярной системе координат имеют вид r = 2Rcos[s(t)/(2R)y, ф = 5(/)/(2Л). Уравнение траектории будет r = 2Rcos(p. При этом диап?ооны изменения полярных координат точки М следующие: SR<r<2R; -п/4<ц><п/4. Читателю предоставляется возможность самостоятельно решить вопрос о целесообразности и трудоемкости определения кинематических характеристик движения точки в задачах, рассмотренных в примерах 1.1-1.5, для разных способов задания ее движения. Глава 2 ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 2Л. Степени свободы и теорема о проекциях скоростей Кинематика твердого тела - раздел кинематики, в котором изучают кинематику абсолютно твердого тела. Основным свойством твердого тела является неизменность расстояния между любыми его точками. В кинематике форма твердого тела не влияет на кинематические параметры его движения, и в данном случае можно использовать аксиому неограниченного распгарения тела, полагая, что в движение вместе с ним увлекаются любые точки из примыкающей области пространства, так что ик также можно отнести к рассматриваемому твердому телу. Задачи кинематики твердого тела сводятся к разработке способов задания его движения, определению на этой основе характеристик движений самого тела и отдельных точек, ему принад-лежащик. Для задания движения твердого тела необходимо прежде всего установить число степеней свободы, т, е. минимальное число независимых скалярных переменных, в совокупности однозначно определяющих положение материального тела в пространстве. В гл. 1 данного раздела показано, например, что для однозначного определения положения точки в пространстве в общем случае надо знать три ее координаты (декартовы или криволинейные), и, следовательно, свободная материальная точка имеет три степени свободы. При движении на плоскости требуются две * Эти переменные называются также обобщенными координатами. координаты, однозначно определяющие положение точки на этой плоскости; в этом случае материальная точка имеет две степени свободы. Наконец, при движении точки по заданной траектории одна координата определяет ее положение на траектории; в этом случае точка имеет одну степень свободы. При задании движения твердого тела следует исходить из того, что его положение в пространстве можно считать определенным, если известно положение трех его точек, не лежащих на одной прямой, например А, В, С (рис. 2.1). В таком случае для однозначного определения положения твердого тела в пространстве необходимо знать по три координаты каждой из этих точек, т. е. для точек А, ВиС нужно знать дс, , , дс, у, Ус 9 Однако все эти девять параметров нельзя считать независимыми, так как координаты тех же точек твердого тела будут связаны тремя уравнениями, вытекающими цз условия неизменности расстояния между точками в твердом теле: (ха-xf +{yj,-yf + (z -z)2 =Z; ixa-xcf -{Уа-ycf -(a-cf =4c; ixc-xf -iyc-Ув? +(c b? I\c> где , Ljc, - расстояния между соответствующими точками в теле. 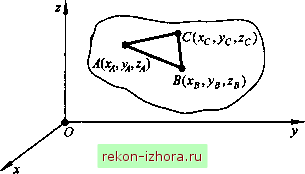
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |