

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Теоретическая механика Так как диссипативная функция Рэлея уже содержит величины второго порядка малости (произведения скоростей обобщенных координат), в разложении в ряд Маклорена, как и в разложении коэффициентов A-j, будем учитывать только первые члены разложения - значения коэффициентов Bj в положении равновесия. Обозначим {B-j)q через bj и назовем их обобщенными due-сипативными коэффициентами, причем Ь = . Тогда 1=1 7=1 В общем случае Ф представляет собой, согласно (19.86), неотрицательную квадратичную форму. Если же Ф является положительно-определенной квадратичной формой, диссипация называется полной. Подставив выражение для диссипативной функции (19.87) в (19.85), получим составляющую обобщенной силы от диссипативных сил: бщ=-1Ь,9,. (19.88) Составляющую обобщенной силы Q{t) от сил Pit), зависящих от времени и действующих на систему извне, можно получить стандартным способом, полагая, что вариация только /-й обобщенной координаты ЬдфО, вычисляя сумму элементарных работ от сил (О на перемещениях, определяемых 5, и относя полученное значение работы к вариации обобщенной координаты: 6,(0 = =-. (19.89) Подставив вьфажения (19.77), (19.84), (19.88), (19.89) для бш бд Gi(0 в уравнения Лагранжа второго рода (19.74), получим в самом общем случае уравнения малых колебаний линейной системы с п степенями свободы*: Z(M.+My+s y) = e/W 0* = Ь2,....,п). (19.90) В частном случае системы с двумя степенями свободы квадратичные формы Г, Я и Ф будут соответственно 1 = (ll9 +2Ci2?l92 +222); (19.91) а дифференциальные уравнения малых колебаний примут вид 111 + 122 +111 +bi22 +111 +122 =Gl(0; 121 + 222 +121 +2292 +121 +222 =62(0- (19.92)  Рис. 19.27 Пример 19.8. Два одинаковых математических маятника длиной / и массой т каждый соединены между собой пружиной, жесткость которой с (рис. 19.27). При вертикальном положении маятников пружина не деформирована. Составить дифференциальные уравнения малых колебаний. Решение. Воспользуемся уравнениями Лагранжа второго рода. В качестве обобщенных координат выберем углы отклонения маятников от вертикали ф и \/. Кинетическая энергия системы Следовательно, в соответствии с (19.91) * При выводе дифференциальных уравнений малых колебаний в линейной системе с п степенями свободы мы воспользовались уравнениями Лагранжа второго рода. Иногда этот способ называют основным способом составления уравнений движения. Аналогичные по структуре (19.90) уравнения можно получить прямым способом: описывая движения входящих в систему инерционных объектов, используя дифференциальные уравнения поступательного, вращательного, плоского и т. д. движений. 11 =22 Потенциальная энергия системы (19.93) Я = mgl(l - cos ф) + mgl(\ - cos \f) + -j сХ , где X -деформация пружины. С учетом малости колебаний со8ф = 1-ф/2, cos\/ = l~\j 2 , Х = /ф-/у. Тогда Я = т/фЧт/у+~с(/\/--/ф)2=1[(т/ + с/Ъф-2с/ФУ+(т Следовательно, в соответствии с (19.91) и дифференциальные уравнения малых колебаний имеют вид т/ф+(mg/ + cl )ф- с/V = 0; m/vjir - с/ф+(mg/ + с/ )\/ = 0. Пример 19.9. Двойной математический маятник (рис. 19.28) состоит из двух связанных шарнирно одинаковых математических маятников массой т и длиной /. К верхнему маятнику приложена горизонтальная сила F(t), При движении на грузы маятников действуют силы вязкого сопротивления F-hv , где h - коэффициент вязкого сопротивления; v - скорость движения груза. Составить дифференциальные уравнения малых колебаний. Решение. Воспользуемся уравнениями Лагранжа второго рода. В качестве обобщенных координат выберем углы отклонения ф и \/ маятников от вертикали. Кинетическая энергия системы 2 2 где Уд =/ф; vs =v +Vba; ва =/у. Согласно теореме косинусов, =(/ф) +(/\/)Ч2/ф\/С08(\/-ф) . Поскольку в выражении для кинетической энергии при малых колебаниях нужно учитывать члены до второго порядка малости, со8(\/-ф) заменяем единицей. Тогда 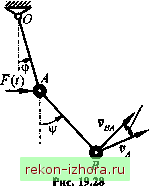
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |