Здесь следует напомнить, что производная от единичного вектора т по скалярному аргументу s есть вектор, перпендикулярный X и направленный по нормали к касательной траектории движения точки в сторону ее вогнутости. Модуль этой производной равен кривизне кривой в данной точке:

где p - радиус кривизны траектории в данной точке.

Тогда единичный вектор п, задающий положительное направление нормальной оси, может быть определен так:

= 1.

dx п= - р =

Вектор n лежит в соприкасающейся плоскости и направлен по главной нормали в сторону вогнутости траектории к центру ее кривизны в данной точке.

Третья ось естественной системы называется бинормальной осью (бинормалью). Она перпендикулярна к касательной и нормальной осям, а ее положительное направление можно найти по единичному вектору бинормали b , который определяется как результат векторного произведения единичных векторов т и п в виде

Ь=ххп , 11=1.

Таким образом, векторный базис х, п и b определяет положительные направления соответствующих координатных осей в каждой точке траектории.

Оси естественной системы (касательная [т], нормаль [п] и бинормаль Щ), построенные в точке М траектории, образуют естественный трехгранник. Грани его, определяемые каждой парой пересекающихся осей, совпадают с соприкасающейся (т, п), нормальной in, Ъ) и спрямляющей, или касательной, {Ь, х) плоскостями (рис. 1.10). При движении точки Мпо своей траектории естественный трехгранник с вершиной в точке М также движется и ориентация его граней и осей, их образующих, изменяется в пространстве.

Нормальная плоскость

Соприкасающаяся плоскость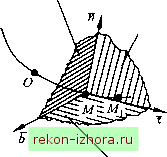

Спрямляющая плоскость

Рис. 1.10

Теперь можно перейти к определению скорости при естественном способе задания движения точки. Согласно основному определению скорости (1.1) и (1.51),

- dr dr ds dr . dt ds dt ds

или, с учетом определения единичного вектора x = dr/ds,

v = iT. (1.52)

Из (1.52) следует, что проекция скорости точки на ось, касательную к траектории точки, равна

Очевидно, что v = = vf.

При v=s>0 точка движется в положительном направлении отсчета s, а при v=s<0 - в противоположную сторону.

Модуль скорости, т. е. ее численное значение, при естественном способе задания движения точки определяется так:

Для ускорения на основании (1.3) имеем

dv d(vJt) rfv- dx .. .dx a =-= -i-LJi = -T + v,- = 5X4--,

dt dt dt dt dt

dx dx ds ds I

где - =---=--- .

dt ds dt dt p

Таким образом,

- s

a=sx + - n ,

(1.53)

a =vT + -n . P

Из (1.53) следует, что ускорение представляет собой сумму

s

касательной cl=sx и нормальной а =-п составляющих (рис. 1.11): J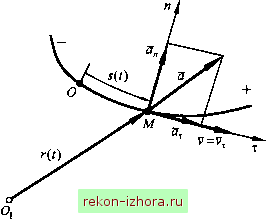

Рис. 1.11

Полученный результат подтверждает вывод о том, что вектор а лежит в соприкасающейся плоскости (х, w) (см. § 1.2). Проекции ускорения на оси естественной системы координат (касательйую, нормаль и бинормаль) равны