Тогда

Логарифмическим декрементом колебаний 5 называют натуральный логарифм от декремента колебаний:

5 = 1пА = 8г1.

Логарифмический декремент колебаний удобен для характеристики медленно затухающих колебаний, когда 8 со. Тогда изменение максимальных значений за условный период мало:

М =4-4,1 4, (19.36)

5 = 1п- = 1п-- = -1п

4+1 4-м

Логарифмический декремент колебаний в этом случае характеризует относительное изменение максимальных значений за условный период. Кроме того, он имеет определенный энергетический смысл.

Вычислим изменение полной механической энергии за условный период колебаний. В положениях максимальных отклонений ((/,) = 0) полная механическая энергия определяется потенциальной энергией

/-/-- /+1-1+1---

С учетом (19.36) для медлешю затухающих колебаний

с(Л-24М) А+1---

Тогда относительное изменение полной механической энергии системы за условный период колебаний будет равно

где \/ - коэффициент поглощения энергии за один период (цикл) колебаний.

2. Случай критического сопротивления: 8 = со; А 2 = -s

При кратных корнях общее решение дифференциального уравнения (19.32) имеет вид

q = C,e- +C,te- = (С, +C,t), (19.37)

Произвольные постоянные определим из начальных условий (19.29):

С, =9о; c2=9o+S9o. (19.38)

Решение (19.37) представляет собой произведение экспоненты в отрицательной степени и линейной функции времени. Из математики известно, что экспонента в отрицательной степени убывает быстрее, чем возрастает любая степенная функция. Поэтому решение (19.37) стремится к нулю при -> оо.

Решение может обратиться в нуль только единожды, если константы С, и С2 имеют разные знаки. Для этого, согласно (19.38), начальное отклонение и начальная скорость должны иметь разные знаки, и при этом необходимо выполнение условия о > z\qQ .

На рис. 19.8 представлено решение (19.37) при различных начальных условиях. Видно, что движение не имеет колебательного характера и отсутствуют какие-либо признаки периодичности. Такое движение называют апериодическим, а с учетом рассмотрения критического сопротивления - предельно апериодическим.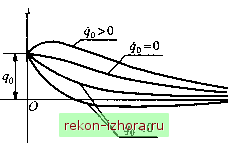

Рис. 19.8

3. Случай большого сопротивления: 8>со; А,2=- 6±А:,

где к = Ve -со . Поскольку к<г, оба корня характеристического уравнения будут отрицательными.

Общее решение дифференциального уравнения (19.32) в этом случае имеет вид

Произвольные постоянные С, и С2 определим из начальных условий (19.29)

с, л

9о +

Яо+Яо

Движение в случае сопротивления, большего критического, также имеет апериодический характер, аналогичный представленному на рис. 19.8, однако с увеличением 8 графики растягиваются вдоль оси абсцисс, поскольку с возрастанием вязкого сопротивления при прочих равных условиях скорость движения убывает.

Пример 19.5. Груз массой /и = 0,5 кг, скрепленный с пружиной, помещен в сосуд с жидкостью, создающей при движении фуза силу сопротивления, пропорциональную его скорости v ( рис. 19.9, л). Определить закон движения груза, если статическая деформация пружины А. = 5 см , коэффициент вязкого сопротивления жидкости /? = 1 Нс/м, а в начальный момент времени фуз был подвешен к концу недеформированной пружины и отпущен без начальной скорости.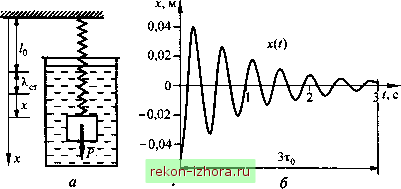

Рис. 19.9

Решение. Дифференциальное уравнение движения груза, скрепленного с пружиной и преодолевающего вязкое сопротивление среды, было получено в примере 19.1. Положив внешнюю силу равной нулю, запишем