Свободные движения линейной неконсервативной системы

В самом общем случае дифференщ1альное уравнение свободного движения такой системы в соответствии с (19.26) имеет вид

q + 2zq + (iiq = Q, (19.32)

где 8 = й/2а - коэффициент затухания, единица измерения которого (рад/с) совпадает с единицей измерения со.

Представив решение уравнения (19.32) в виде q = e, получим характеристическое уравнение

-hleX-hco =0,

корни которого

>.i2=-s±Vs-a) . (19.33)

Характер движения системы будет существенно зависеть от соотношения между величинами 8 и со. Возможны следующие три случая:

при 8 < со - случай малого сопротивления - уравнение (19.33) имеет комплексно-сопряжеитые корни;

при 8 = со - случай критического сопротивления - уравнение (19.33) имеет кратные корни;

при 8 > со - случай большого сопротивления - уравнение (19.33) имеет два вещественных отрицательных корня.

Рассмотрим эти случаи по отдельности.

1. Случай малого сопротивления: 8 < со; А 2 = -е ± ,

где coi = л/со -8 .

Общее решение дифференциального уравнения (19.32) будет иметь вид

q = e (Ci cos coj/ + Cj sin (ot),

qAesmicot--a). (19.34)

При начальных условиях (19.29)

C,=g,; C,=, (19.35)

откуда, согласно (19.30), находим А =

а = arctg-

Яо-Яо

При определении а следует учитывать, что при qQ +sqQ>0 а находится в I или IV квадранте, а при qo +sqQ<0 - во II или III и, следовательно, к вычисленному главному значению арктангенса необходимо добавить п. При +9о =0 а = я/2, если 9о >О, и а = -7г/2, если qo <0.

Графически решение (19.34) приведено на рис. 19.7. Оно представляет собой синусоидальную кривую, расположенную

между экспоненциальными ограничивающими кривыми Ае и

-Ае . Колебания такого вида называются затухающими,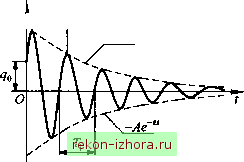

Рис. 19.7

Затухающие колебания не являются периодическим движением, однако сохраняют его некоторые свойства. Действительно, решение (19.34) представляет собой произведение двух функций - экспоненты, которая не обращается в нуль, и синусоиды с периодом Т; = 27г/(о, . Это обстоятельство приводит к чередованию через равный промежуток времени 7J нулей и максимумов q(t) (см.

рис. 19.7), что позволяет считать затухающие колебания условно-периодическими.

Величину Г, =2я/а) = 2п/Vco -8 называютслмльш периодом затухающих колебаний. Условный период затухающих

колебаний больше периода свободных колебаний консервативной системы Т.

Величину coi называют условной частотой затухающих

колебаний. Отметим, что при малых значениях коэффюдаента затухания (8 а)) условная частота затухающих колебаний coj (О; аналогично ТТ.

Наконец, величину Ае можно назвать условной амплитудой затухающих колебаний.

Решение (19.34) показывает, что затухающие колебания должны продолжаться сколь угодно долго, поскольку q{t) обращается в нуль только при /->оо. Однако это не соответствует опыту наблюдения колебаний в реальных системах, которые всегда заканчиваются за конечный промежуток времени. Данное противоречие есть результат того, что в расчетной схеме не учитывались другие виды сопротивлений, кроме линейно-вязкого. Ниже будет показано, что учет сил сухого трения приводит к прекращению колебаний через конечный промежуток времени.

Величина Xq=1/s называется постоянной времени затухающих колебаний и измеряется в секундах. Рассмотрим последовательность условных амплитуд колебаний в моменты времени, отличающиеся один от другого на постоянную времени Xq :

ААе у А Ае -А-е ; А -А-е ....

За каждый промежуток времени Xq условная амплитуда затухающих колебаний уменьшается в е раз. Через Зхо условная амплитуда уменьшится в , т. е. примерно в 20 раз. Обычно полагают, что по истечении времени, равного Зхо, затухающие колебания можно условно считать прекратившимися.

Декрементом колебаний А называют отношение двух последовательных (взятых через условный период Т) максимальных значений обобщенной координаты. Пусть 4 = Ае sin(a)i, + а);

.,1 = Ае- sin[a)i (/, + Ti) + а] = Ае sin(a)i/,- + а), где - время, соответствующее /-му максимуму координаты.