

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Теоретическая механика f = e = - = ; ( .22) п dt dt dq dt dt Подставив (19.22) и (19.23) в (19.21), получим dT dn - = ---2Ф, dt dt dt dt тцсЕ- полная механическая энергия. Таким образом, удвоенное значение диссипативной функции Рэлея есть скорость уменьшения полной механической энергии системы. Составляющую обобщенной силы от сил Pit), зависящих от времени и действующих на систему извне, можно получить стандартным способом, полагая, что вариация обобщеишой координаты 5 не равна нулю, вычисляя сумму элементарных работ от сил Р, (t) на перемещениях, определяемых 5, и относя полученное значение к 5: Учитывая (19.13), (19.14), (19.16), (19.19), (19.20) и (19.24), запишем уравнение Лагранжа второго рода в виде £(дТ ЭФ ЭЯ , ++3-=б(0, dq dq aq + bq + cq = Q(t), (19.25) где a>0;fc>0;c>0. Уравнение (19.25) представляет собой дифференциальное уравнение малых колебаний любой линейной колебательной системы с одной степенью свободы. Разделив каждый член этого уравнения на обобщенный инерционный коэффициент а , получим по аналогии с рассмотренными выше примерами q + 2zq + (iiq = - Q(t), . (19.26) где 2г = Ь/а; со =с/а. 19.3. Свободные движения линейной системы с одной степенью свободы Свободные движения в колебательной системе возникают при отсутствии внешнего воздействия (Q(t) = О) после начального возмущения. В соответствии с (19.25) дифференциальное уравнение движения в этом случае имеет вид aq + bq + cq = 0. Свободные колебания линейной консервативной системы В случае консервативной системы Ь = 0, поэтому дифференциальное уравнение движения принимает форму 9 + со9 = 0, (19.27) где со =с/а . Запишем решение уравнения (19.27) в виде 9 = С, COSC0/ + C2 sin со/. (19.28) Произвольные постоянные С, и С2 определим из начальных условий: при/ = 0 9 = 9о. Я = Яо (19.29) Отсюда Введем новые произвольные постоянные A = yjc[7cf; a = arctg (19.30) и представим решение (19.28) в так называемой амплитудной форме: q = As\n((ot + a), (19.31) Произвольные постоянные А и а в соответствии с (19.30) выражаются через начальные условия следующим образом: а = arctg При определении а следует учитывать, что если jq > О, то а находится в I или IV квадранте, а если qQ<Q - то во П или Ш, и, следовательно, к вычисленному главному значению арктангенса необходимо добавить п. При 0= а = л;/2, если до >О, и а = -л;/2, если д<0. Зависимость q{t) представлена на рис. 19.5. 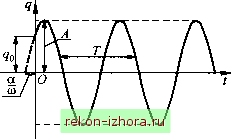 Рис. 19.5 Гармоническими называют такие колебанры, при которых обобщенная координата изменяется во времени по закону синуса или косинуса. Как следует из (19.28) и (19.31), свободные колебания линейной консервативной системы с одной степенью свободы являются гармоническими. Их характеристиками являются: со - круговая, или циклическая частота, измеряемая в се- к)шдах в минус первой степени (с~); ш + а - фаза колебаний, а - начальная фаза колебаний; А - амплитуда колебаний; Т- период колебаний - время в секундах, за которое фаза колебаний изменится на 2п Т = 2п/(0=2п[а/с ,
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |