координаты точек которой удовлетворяют голономным связям, наложенным на систему. В момент времени / положение точки

определяется радиус-вектором F/(/), а в момент времени t + dt - радиус- вектором

+dt)=F;(t)+v;{t)dt + -a;{t)dt +(I8.21)

где vCOj k(0 - кинематически возможные скорость и ускорение кй точки системы в момент времени t.

Положим, что r(0 = V*(0- Тогда, вычитая (18.20) из (18.21), получим следующее выражение для возможного перемещения точки:

5F, = F; (t + dt) -r,it + dt) = [v; (0 - V, (0] dt + + [a:it)-a,{t)]dt+....

(18.22)

Если (t) = (t), to, пренебрегая в правой части (18.22) слагаемыми, содержащими dt в третьей и более высоких степенях, находим:

Подставив (18.23) в общее уравнение динамики (18.15) и разделив обе части выражения на , получаем

br,=bd,dt\

(18.23)

(18.24)

Массы точек и приложенные к системе активные силы заданы и не изменяются, поэтому

5а, =-6

Подставляя вариацию ускорения Ъа в (18.24), находим

- - (р Л

к=\ \Щ

л=1

= 0.

Выражение

л=1 2

к -

= Z введено Гауссом и назы-

вается принуждением. Принуждение является мерой отклонения действительного движения от того движения, которое совершала бы данная система, если начиная с некоторого момента времени она двигалась под действием только активных сил, а связи были бы отброшены. Условие (18.24) можно записать так:

5Z = 0.

Принцип Гаусса формулируется так: при действительном движении механической системы с идеальными связями принуждение Z принимает значение, наименьшее из всех возможных значений при движениях, совместимых с наложенными связями.

Принцип Гаусса можно рассматривать как модификацию принципа Даламбера-Лагранжа, в которой используется понятие экстремальности некоторого выражения, называемого принуждением.

Пример 18.11. Определить ускорение материальной точки, которая движется под действием силы тяжести по гладкой плоскости, наклоненной под углом а к горизонту (рис. 18.16). Начальная скорость точки равна нулю.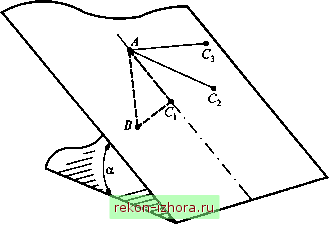

Производная

если

Решение. Возможные траектории точки располагаются в наклонной плоскости, и возможные перемещения /1С/=-а,5г. При свободном движении под действием силы тяжести перемещение точки за такой же промежуток времени равно AB=g8t. Наименьшим из отрезков АС/ будет отрезок , расположенный вдоль линии наименьшего ската. Так как

ACiafit и AC=ABsma = gSlnaЪt,

а, =gsina .

Такой же результат можно получить при использовании принуждения. Для данной задачи оно пропорционально квадрату длины отрезка 5С,:

л, =gsina .

18.5. Уравнения Лагранжа второго рода

Вывод уравнений

Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения движения несвободной механической системы, составленные в обобщенных координатах. Рассмотрим движение системы, состоящей из N материальных точек, относительно инерциальной системы отсчета. Наложенные на систему связи - голономные, удерживающие, идеальные. Если некоторые связи не идеальные, то соответствующие им реакции следует добавить к действующим на систему активным силам.

Общее уравнение динамики для такой системы имеет вид

1№-ад)бг,=0. (18.25)