

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Теоретическая механика 14.7. Эллипсоид инерции. Главные оси инерции Эллипсоид инерции - поверхность второго порядка, построенная в любой точке тела - характеризует спектр моментов инерции тела относительно осей, проходящих через эту точку. Для построения этой поверхности на каждой оси О/, проходящей через точку О, откладывают от этой точки отрезок оа: = 1/7л Геометрическое место концов отрезков ОК (точек К) и является эллипсоидом инерции. Получим уравнение эллипсоида инерции в системе координат Oxyz (рис. 14.18). Подставив выражения cosa = xjOK = yjJiX, cos = у/ОК = yfjy, cosy = z/OK = Jj)z в формулу (14.13), получим jy+jy -lJyXy-lJz-lJyyz\. (14.15) 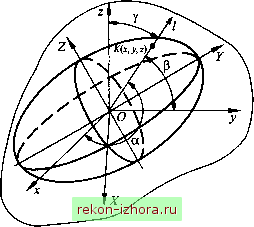 Рис. 14.18 Выражение (14.15) - это уравнение центральной поверхности, не имеющей бесконечно удаленных точек, так как для всех осей отрезок ОК имеет конечную длину. Такая поверхность и есть эллипсоид инерции. Для бесконечно тонкого тела в виде прямолинейного отрезка эллипсоид инерции вырождается в цилиндр, если точка о принадлежит отрезку или прямой, содержащей этот отрезок. Для каждой точки тела существует свой эллипсоид инерции. Если оси координат направить по взаимно перпендикулярным главным осям эллипсоида инерции (ох, 0Y, 0Z на рис. 14.18), то его уравнение будет иметь следующий вид: JX +JyY +JzZ =1. (14.16) Главные оси (оси симметрии) эллипсоида инерции, построенного в точке твердого тела, называются главными осями инерции для данной точки тела. Следовательно, в каждой точке тела имеются три главные оси инерции, которые являются главными осями эллипсоида инерции, построенного в данной точке. Эллипсоид инерции, построенный для центра масс тела, называется центральным эллипсоидом инерции, а его главные оси - главными центральными осями инерции тела. Моменты инерции тела относительно главных осей инерции в точке называются главными моментами инерции для этой точки тела. В формуле (14.16) это J, Jy, Jz- Моменты инерции относительно главных центральных осей инерции называют главными центральными моментами инерции тела и обозначают J , , . Сравнив уравнение (14.16) с уравнением эллипсоида инерции, записанным в канонической форме: X Y а Ь с = 1, (14.17) получим а = -7=; Ь=-=: с = - т. е. большей оси эллипсоида инерции соответствует меньший главный момент инерции тела для данной точки. Эллипсоид инерции называется трехосньш, если все главные моменты инерции для точки тела разли11ны, и эллипсоидом вращения, если два главных момента инерции для точки тела равны. Все прямые, расположенные в плоскости, перпендику- лярной оси вращения, являются главными осями инерции тела в точке. Эллипсоид инерции становится сферой, если все главные моменты инерции тела в точке равны. Все оси инерции, проходящие через центр сферы, являются главными. Уравнения эллипсоида инерции (14.16), (14.17) не содержат центробежных моментов инерции, т. е. центробежные моменты инерции относительно главных осей инерции равны нулю: Jxy=Jxz-Jyz=- (14.18) Справедливо и обратное утверждение: чтобы оси прямоугольной системы координат были главными осями инерции, необходимо и достаточно выполнить условия (14.18). Запишем формулу (14.13), когда оси ОХ, 0Y, OZ являются главными осями инерции в точке О. В этом случае все центробежные моменты инерции равны нулю и J/ = Jx cos a-Jy cos + Jz os у. (14.19) С помощью этой формулы при известных главных моментах инерции в точке О определяют момент инерции относительно оси 01. Моменты инерции относительно произвольной оси 01 (рис. 14.19), согласно выражению (14.19) и теореме Гюйгенса-Штейнера, вычисляют по формуле У/ = + Md = Jx cos а + J.j, cos p + J. cos у + Md, 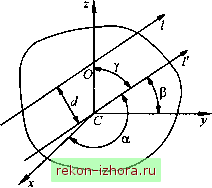
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |