

 |
 |
Разделы сайта
Читаемое
Обновления Aug-2025
|
Промышленность Ижоры --> Динамика жидкости: уравнения трех компонент скорости. Как правило, они получаются из решения укороченных уравнений, пригодных для определения начального положения [Blottner, 1975а]. 15.4.L Квазихарактеристическое поведение Из уравнений (15.84)-(15.86) следует, что вдоль направлений X и Z существует лишь конвективный перенос; вдоль направления у - конвекция и диффузия. Формально (т. е. согласно процедуре, описанной в гл. 2) уравнения (15.84) - (15.86) Область зависимости Область влияния  Поверхность гела Рис. 15.21. Области влияния и зависимости. являются неэллиптическими. Кроме того, возможно ввести квазихарактеристики, связанные с конвективным оператором (в пренебрежении нормальной компонентой v скорости течения) д д , (15.87) Квазихарактеристическое направление определяется проекцией линии тока на плоскость, касательную к поверхности тела, т. е. dz/dx = w/u. Но w/u изменяется поперек пограничного слоя. Поскольку при заданных (х, г) возмущения в направлении у распространяются по всей области, необходимо определить области зависимости и влияния (рис. 15.21). Возмущения в некоторой точке Р внутри пограничного слоя будут воздействовать на всю область, расположенную вниз по потоку и ограниченную плоскостями, проходящими через нормаль к телу, проведенную через точку Р; причем одна плоскость проходит через предельную линию тока на твердой поверхности, а другая через проекцию линии тока, расположенную на внешней границе пограничного слоя. Гиперболичность задачи в плоскости (дс, z) существенно ограничивает область, в которой по заданным начальным данным может быть найдено решение. Если начальные данные Uo(y) и Woiy) определены на поверхности Si, перпендикулярной стенке (рис. 15.22), решение вниз по потоку может быть 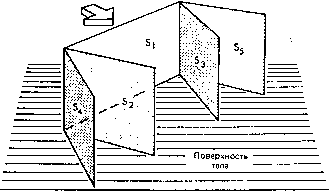 Рис. 15.22. Начальные и граничные данные. получено лишь в области, ограниченной квазихарактеристиками S2 и S3 (и твердой стенкой и внешней границей пограничного слоя). Квазихарактеристические направления S2 и S3 определяются либо направлением предельных линий тока на стенке, либо направлением линий тока на внешней границе слоя. Попытки определить решение слева от S2 или справа от S3 (если смотреть против потока) нарушают принцип влияния Рэтца [Krause, 1973], поскольку локальное решение в этих областях определяется данными, лежащими вне плоскости Si. Как отмечено в п. 2.2.3, если определить дополнительные граничные условия, например на поверхностях S4 или S5, решение можно получить в любой области вниз по потоку, ограниченной начальными и граничными условиями. С вычислительной точки зрения гиперболичность особенно существенна при построении явных маршевых алгоритмов в направлении г. Как и для двумерных пограничных слоев, для дискретизации в направлении у существуют практически универсальные неявные схемы. Чтобы численное решение было устойчиво, должно выполняться условие Куранта -Фридрихса -Леви (КФЛ) (п. 9.1.2), согласно которому расчетная область зависимости в плоскости (x,z) должна включать в себя физическую область зависимости, определяемую уравнениями в частных производных. Это существенно ограничивает относительные размеры шагов Ах и Az [Krause, 1973]. При сравнении различных схем будет предполагаться, что X примерно совпадает с направлением невязкого течения, а г направлено поперек потока, например в направлении размаха 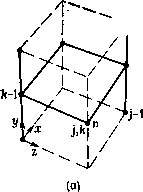 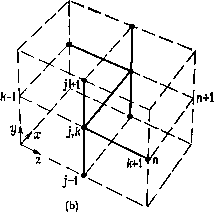 Рис. 15.23. Точки сетки, задействованные в схеме; (а) схема Кранка - Николсона, (Ь) схема загзаг Краузе. крыла. При рассмотрении х в качестве первоначального маршевого направления скорость и предполагается положительной, а W может быть как положительной, так и отрицательной величиной. Прямое обобщение схемы Кранка - Николсона на случай трех пространственных переменных состоит в центральной дискретизации в точке {k-1/2, п+1/2) в плоскости z (рис. 15.23) и в построении двух трехдиагональных систем разностных уравнений для и и w из уравнений х- и г-компонент импульса вдоль линий сетки (k, n+l), т. е. в направлении у. Из условия КФЛ следует, что скорость w должна быть положительна и Ах ограничено условием \wAx/uAz\l. Узлы сетки для трехмерной схемы Кранка - Николсона показаны на рис. 15.23. Проход по Z осуществляется в направлении увеличения k. Если W везде меньше нуля, проход по z осуществляется в направлении уменьшающихся значений k. Таким образом, при-
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |