15.2.3, Связанная схема Дэвиса

В данном разделе будет описана связанная схема Дэвиса (DCS) решения системы (15.38) - (15.40) для несжимаемого пограничного слоя. В этом случае /=1, 9=1 и необходимо рассмотреть лишь уравнения (15.38), (15.39). Применение схемы DCS рекомендуется Блотнером [Blottner, 1975b] после проведенного им сравнения по точности и эффективности ряда

1-1

Рис. 15.7. Сетка в пограничном слое в пространстве (g, т]).

схем Кранка - Николсона. Термин связанная объясняется одновременным неявным рассмотрением уравнений неразрывности и х-компоненты импульса в противоположность последовательному решению уравнений (15.7), (15.8). Если (15.39) записать в виде

= RHS = -l/--P(/-l) + l-, (15.43)

ТО, используя разностную схему Кранка -Николсона в узле (п-f 1/2,/), можно построить маршевый алгоритм (здесь RHS означает правая часть уравнения ). Другими словами, (15.43) заменяется выражением

0.5(Г + Г0 д = 0.5(RHS + RHSO. (15.44)

Производные по г] в (15.43). аппроксимируются трехточечными центральными разностями (рис. 15.7). Нелинейные неявные члены в (15.43) и (15.44) линеаризуются разложением Ньютона- Рафсона, т. е.

(15.45)

где итерации по k проводятся на каждом шаге по п в направлении потока. После достижения сходимости по k получается решение на слое /г+1. Подставив (15.45) в (15.44), можно получить линейную относительно f *+ и систему уравнений

aiFi-i + biFi + C1F1+1 + gjVi =di

/ = 2, 3, /-1, (15.46)

P +-д-

cf = -0.5 (1 - 0.5ДГ1 V/). gi = 0.25ЛЛ (Fi -4 = -aFU - cIfUi - [1 + 0.5Ar]YFl] F, +

(2ДТ1)

Уравнение неразрывности (15.38) в разностной форме имеет вид

+ 0.25[(Fr4/il) + (/+/-i)]=0. (15.47) Уравнение (15.47) можно разрешить относительно У* :

1/11 5; {F)l\ + fГ) + / = 2, 3, ..., /, (15.48) где 5, = 2Лл(0.25 + Г+/7А),

= -2аг1 (0.25 - [Ff + - {v) - Kf-,)-

Уравнения (15.46), (15.48) решаются одновременно модифицированным трехдиагональным алгоритмом (п. 6.2.2). Первый проход осуществляется от внешней границы пограничного слоя к стенке. На границе слоя £y=Gy=0, ву = 1.0. При умень-

(15.49)

шающихся значениях / = (/ - 1), (/ - 2), ...

Г = 6/ + CiE,+i + s, (c,G,+, + gi). E, = -[а/ - S/.(cyG/+, + gi)]/T, G/ = -[c/G/+, + g/]/r,

e, = [dj - (ciGj+i + gi) t, - 0,6}+,1T.

Ha стенке Fi = Vi = 0, a для увеличивающихся значений j = = 2, 3, .... /

/ = -1 + G,V, , + e V, = V, , - s, (F/ , + F,) =

(15.50)

Ha практике решение систем (15.46) и (15.48) повторяется до тех пор, пока величины F* * и У/ * не станут равными

10*-

1 Ол1

Одна итерация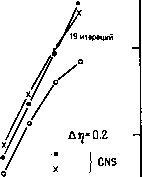

о DCS-B

( одна итерация)

10- Д4

Рис. 15.8. Сходимость схемы DCS ([Blottner, 1975b]; печатается с разрешения North-Holland).