где pdpi - отношение давлений (PRAT в программе SHOCK). Из уравнений (14.169) также следуют граничные условия при х = О yl 1.0. Решите задачу при NX = 101, NT = 170 и DT = 0.100 по схеме Лакса - Вендроффа с искусственной вязкостью. Общий характер решения можно сравнить с численным решением Сода [Sod, 1978]. Точное решение этой задачи можно найти у Липмана и Рошко [Liepmann, Roshko, 1957]. Наибольшую сложность представляют расчет контактного разрыва и ударной волны.

14.9. Получите решение задачи о распространении умеренной {pjp2=2.b, рис. 14.18) и сильной (pjp2 = 10, рис. 14.25) ударных волн по схеме FCT при следующих значениях диффузионных и антидиффузионных параметров в (14.93):

(1) т1о = 0.125, Л1=0. Л2 = 0,

(2) т1о = 0.500, Л1=0, Л2 = 0,

(3) Ло=1/3, Л1 = 1/3, Л2==-1/6,

(4) Ло=1/6, Л1 = 1А Л2 = -1/3. Сравните профили ударных волн, полученные в различных вариантах.

14.10. Примените схему FCT к решению задачи 14.8 об ударной трубе. Сравните полученные решения с решением, найденным по схеме Лакса - Вендроффа с искусственной вязкостью (задача 14.8). Особое внимание уделите профилям ударной волны и контактного разрыва.

Трансзвуковые невязкие течения (§ 14.3)

14.11. Течение у тонкого крыла, задаваемого уравнением у = т{х - \ ), -1 Jc 1, в области, изображенной на рис. 14.34, описывается трансзвуковым уравнением малых возмущений (14.130). Граничные условия приведены на рис. 14.34. Получите численное решение при т = 0.1, == 0.8 и 0.9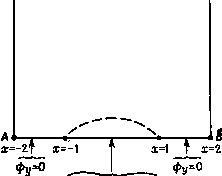

Рис. 14.34. Модельная задача для уравнения потенциала.

на сетке 41 (NX)X 21 (NY). Для конечно-разностной дискретизации используйте формулу (14.135). Для расчета используйте итерационный алгоритм SOR.

14.12. Решите задачу, представленную на рис. 14.34, используя дискретное представление уравнения полного потенциала (14.129), (14.138), (14.139),

Для введения диссипативного механизма в сверхзвуковой области используйте (14.143). Граничное условие Фу = fx на АВ можно трактовать как вдув газа с заданным профилем скорости.

Для решения дискретных уравнений используйте метод приближенной факторизации, подобный (14.156), (14.157), но с использованием метода установления (14.137). Получите решение на сетке 41 (NX)X 21 (NY) при т=0.1 и Моо = 0.8 и 0.9. Сравните полученные решения с решениями задачи 14.11.

14.13. При помощи центральных разностей проведите дискретизацию уравнения Лапласа дФ1дх + дН/ду = О в прямоугольной области О 1, О 1/1 с граничными условиями 0(0, г/) = со8(0.5яг/), 0(1, /) = = ехр(я/2)со5(0.5яг/), ф(х, 0)= ехр(0.5ял:), ф(х, 1) = 0.

Получите решение дискретных уравнений

(1) по схеме приближенной факторизации (14.156), (14.157),

(2) по схеме приближенной факторизации в сочетании с многосеточным подходом (14.156), (14.157), (14.162)

и сравните эффективность методов, принимая во внимание число итераций необходимое для получения сходящегося решения и примерное число операций. Точное решение этой задачи Фех = ехр(0.5ял:)со8(0.5яг/).

14.14. Примените приближенную факторизацию в сочетании с многосеточным подходом на сетке 65X33 к задаче 14.11. Сравните приблизительна эффективность метода с методом, использующим просто приближенную факторизацию на самой мелкой сетке.

Глава 15 Течения в пограничном слое

Течения в пограничном слое традиционно выделяют в отдельную категорию течений (см. табл. 11.4 и § 11.4). Применительно к численным расчетам течение в пограничном слое удобно определить как поток, для которого диффузия, связанная с вязкостью, существенна лишь в направлении, нормальном к поверхности, на которой возникает пограничный слой

u=u=0

Рис. 15.1. Течение в пограничном слое.

{рис. 15.1). Уравнение для нормальной составляющей импульса может быть заменено условием постоянства давления в этом направлении. Если распределение давления известно, то уравнения, описывающие такое течение, перестают быть эллиптическими, что позволяет разработать весьма эффективные одно-проходовые маршевые алгоритмы (в направлении х на рис. 15.1) для их решения.

В пограничных слоях имеют место большие градиенты скорости в направлении, нормальном к поверхности. Поэтому желательно использовать преобразования координат, для которых эти градиенты стали бы меньше в новой системе координат. Наиболее эффективные преобразования описаны в § 15.2 и 15.3. Кроме того, для получения хорошего разрешения вблизи стенки используются сетки, шаг которых геометрически возрастает в направлении нормали к поверхности (п. 15.1.2).

Уравнения, описывающие движение в трехмерном пограничном слое, являются гиперболическими в плоскостях, нормальных к поверхности, на которой развивается пограничный слой. Это усложняет области зависимости и влияния в этих пло-