И, согласно (12.12), А,=11 + Ц, А, = ц1 + ц1, А, = 1,% + 1ц;

J - якобиан (детерминант) преобразования, определяемый выражением (12.3). Метрические коэффициенты, подобные определяются отображением (гл. 13).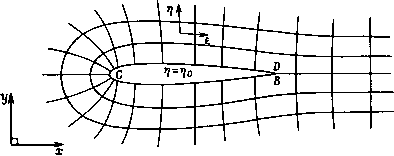

Рис. 14.31. Обобщенные координаты, (а) Физическая область; (Ь) область

расчета.

Уравнение (14.144)1 в дискретном виде записывается аналогично (14.139), т. е.

Ag Ал

= 0. (14.147)

Здесь р* и р* -аппроксимации р* против потока. Так, p*+ij2,k определяется в случае положительной скорости выражением (14.143), в котором следует заменить р на р*. При отрицательном значении f/ используется аналогичная аппроксимация против потока, в которую входит р.з/2, k- Выражения, эквивалентные (14.143) в направлении r](k), используются для аппроксимации р. Направленная против потока аппроксимация плот-

ности позволяет избежать введения дополнительных диссипативных членов, подобных Г/, k в (14.138).

Значения плотности получаются из (14.145), для чего требуется определить /, U, дф/dl и т. д. в полуцелых точках сетки типа {j+ \/2,k). Например,

Ui+lJ2,k 1 J + \l2,k-д--h

+ Лг[.и... . (14.148)

/+1/2. А; + 1 =0.5(/, -f / + 1, k + \).

Таким образом, значения ф хранятся в узлах сетки. Метрические коэффициенты Ль А2, A3 и J аппроксимируются по стандартным формулам второго порядка (п. 12.2.1) и хранятся в полуцелых точках сетки. Для сохранения общей точности важно, чтобы метрические коэффициенты аппроксимировались без осреднения [Flores, 1983].

14.3.5. Решение алгебраических уравнений

Для решения алгебраических уравнений, возникающих при дискретизации уравнений типа (14.130) и (14.137), можно использовать модификацию метода SOR (§ 6.3), получившую название метода последовательной линейной верхней релаксации SLOR. Методом SLOR (см., например, (6.64), (6.65)) на {п-{-1)й итерации решается неявная система, определяющая поправки к решению, A V = yV на каждой координатной линии у (линии постоянного значения /). Для этого используется метод решения систем с трехдиагональными матрицами (см. п. 6.2.3) \

В дозвуковой области для определения A/.V> помимо значений потенциала ф на /-й линии сетки, нужно знать величины ф1~\,к и ф]tl,ky В сверхзвуковой области, помимо значений потенциала ф на /-Й линии, нужно знать величины ф]-2, k и ф-], Такая схема хорошо работает при решении трансзвукового уравнения малых возмущений [Murman, 1973]; в случае решения уравнения для полного потенциала она должна быть несколько модифицирована.

Полезно представить схему релаксации в общем виде, т. е. в виде, аналогичном (6.51),

NAsJ+ = (oR, (14.149)

Метод прогонки. - Прим. ред. 15 К. Флетчер, т. 2

где Ф - вектор значений у, k в точках сетки, R - остаток, полученный при подстановке ф в разностные уравнения, со - масштабный множитель, а N - линейный разностный легко фак-торизуемый (обращаемый) оператор. Если N является достаточно близкой аппроксимацией R, то скорость сходимости к решению будет высокой.

Эквивалентной зависящей от времени интерпретацией является соотношение

*1г + *(-) = 0 (14.150)

где L - оператор стационарного дифференциального уравнения, которое следует решить. Сравнение (14.149) и (14.150) позволяет установить соответствие

КЬф, Аф = М. N = . (14.151)

Следовательно, N следует выбирать так, чтобы соотношение (14.150) представляло сходящийся и зависящий от времени процесс.

Основываясь на этом подходе, типичную схему релаксации для решения уравнения (14.126), дискретизированного центральными разностями в дозвуковой области и с помощью формул (14.142) в сверхзвуковой, можно представить в виде

+ ТзДУ = /?у,ь (14.152)

где Т1=1/Дл:2, т2=1/Ду2, Тз = (2/(о-l)(ti-f tg); со -параметр релаксации. В работе [Jameson, 1978] показано, что фактически по данной схеме решается уравнение

(1 - М2)> + Фпп = Mst + 2Р , + УФи (14.153)

где а, р и 7 зависят от ti, Т2 и тз. Уравнение (14.152) эффективно при расчете дозвуковых областей. В сверхзвуковых областях, чтобы сделать матрицу N в (14.152) с диагональным преобладанием, аппроксимацию фхх, фху и фуу необходимо провести так, чтобы член (1-М)фз8 в (14.153) имел вид

(1-М2) + 2()(1М2){ + -} . (14.154)

Аналогичный подход введения зависимости от времени, эквивалентный (14.150), эффективен и при рассмотрении закона сохранения (14.137). Методы релаксации очень быстро сходятся в начале решения, но, как отмечено в п. 6.3.5, скорость сходимости сильно уменьшается при приближении к стационарному состоянию.