сеток. Распределение точек сетки в направлении третьей переменной в этом случае может быть не слишком гладким [Thompson, 1984].

13.2.5, Сетки, близкие к ортогональным

Строго ортогональные сетки позволяют избавиться от определенных членов в уравнениях движения (п. 12.1.3). Вместе с тем сетки, близкие к ортогональным, строить значительно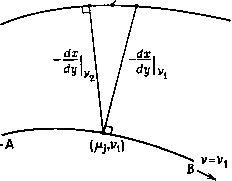

Рис. 13.17. Построение приближенно ортогональной сетки.

Проще. Их Применение позволяет избавиться от ошибок, связанных с деформацией сетки.

Ниже описывается метод построения сетки, близкой к ортогональной. Предполагается, что семейство линий, изображенных на рис. 13.16, построено. Как и в п. 13.2.4, процедура начинается с определения точки \i=\Xj на ABC. Данная процедура является схемой предиктор - корректор, позволяющей получить точку на линии v = V2, приблизительно ортогональной линии, на которой лежит точка (р./, vi) (рис. 13.17). Проводится нормаль к линии v = vi до пересечения с линией v = V2. В точке пересечения вычисляется нормаль-dx/dy , и точка пересечения сдвигается до тех пор, пока эта нормаль не пройдет через начальную точку (р./, vi). Конечная точка (р/, V2) на линии V2, ортогонально соответствующая точке (р,/, vi), берется посредине между двумя точками пересечения. Это эквивалентно использованию следующего характеристического направления:

dx dy

vi, n

dx dy

v., n}

(13.34)

l- + -S=( Л), -S- + S = Qa> Л), (13.35)

дх ду~ дх ду

где Р и Q - известные функции, используемые для контроля сгущения внутренних точек сетки.

Использование эллиптических уравнений в частных производных для построения внутренних точек сетки имеет ряд преимуществ. Прежде всего в этом случае сетка изменяется гладко, даже если граница области имеет излом. Если бы для построения внутренних точек сетки использовались гиперболические уравнения в частных производных, все изломы границы проявлялись бы и во внутренних точках.

Эллиптические уравнения, подобные (13.35), при различных ограничениях на Р и Q удовлетворяют принципу максимума, т. е. максимальное и минимальное значения I и ц достигаются на границе. Томпсон [Thompson, 1982] отмечает, что это обычно? гарантирует однозначность отображения. Однако при некото-

После определения всех точек на линии v = V2 процесс повторяется для определения точек приближенно ортогональной сетки на линии v = V3. Процесс продолжается до тех пор, пока не будет достигнута внешняя граница, т. е. ED на рис. 13.16.

Типичная программа расчета пересечения с линией v = V2 оформлена в виде подпрограммы SURCH (см. рис. 13.29). Описанный метод построения сетки был предложен в работе [McNally, 1972].

13,2.6. Решение эллиптических уравнений в частных производных

В данном разделе будут рассмотрены более общие способы, построения координат, не обязательно приводящие к ортогональным или конформным сеткам. Однако эти способы позволяют лучше контролировать сгущение сетки во внутренних точках области.

Как отмечено в начале гл. 13, задача построения внутренних точек сетки может быть поставлена как граничная задача причем постановка в расчетной области (g, т]) предпочтительней. Поскольку нужно решать эллиптические уравнения в частных производных, в качествеграничных условий необходимо задавать либо положение точек, либо наклон координатных линий на границе.

Наиболее общим уравнением в частных производных, используемым для построения сеток, является уравнение Пуассона, записанное в виде системы

рых экстремальных выборах Р и Q возможно локальное самопересечение сетки.

Решение системы (13.35) ищется в расчетной области (g, ц), В этой области (13.35) преобразуется к виду

Здесь a = g22y Р == g i2, У = gn и 8 = g, где gf -определитель метрического тензора (12.12).

Для определения граничных условий, замыкающих систему (13.36), полезно рассмотреть частный пример, приведенный на рис. 13.18. На контуре АВС{АВС) ц = Ц1 и х = хавс(1), у = = УавсЦ) при I Ьу где функциональные зависимости хавс(1) и Уавс(1) известны и определяют распределение точек сетки на ABC. Аналогично на контуре DFIфРЧ) = тг и x = Xdfi{1), У = Уор1 при gi < К I2, тле XDFiil) и уопЦ) определяют распределение точек на DFI. Задача распределения точек сетки по границе облегчается использованием одномерных функций растяжения, описанных в п. 13.3.1.

Следует отметить, что граничные условия не определяются на АГ и CD\ поскольку в физической плоскости соответствующие линии являются внутренними (и совпадают).

Уравнение (13.36а), дискретизованное при помощи центральных разностей, принимает вид

(а:/ 1, k - 2л:д + Xf+i k) - О.бр k+\ - /-1, k+i -

- /+1, ki + fe-i) + y (/, k-i - 2л:д k + fe+i) + + О.ббР (ATy+i, k - /-1, k) + 0.56Q {xj ~ xj k,) = 0, (13.37) где

a = 0.25 [(X/, - xj k,f + (У/, fei - fe,)2], = 0.25 [(xy+i, k - fe) (a:/, k+\ ~ л: fe-i) +

+ (f -.!, fe ~ k) fe+i ~ У/, k-i)l (13.38)

= 0.25 [(jc/i - ,)2 + (у;+ , - ,)2],

б = [(л:/+1, - X/i, fe) (уд - Уд ; ,) -

Уравнение (13.36b) приводится к дискретному виду аналогичным образом. При записи (13.37) и (13.38) предполагалось, что = Ат) = 1. Такой выбор не влияет на сетку в физической области.