

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Динамика жидкости: уравнения границе можно определить х = хь{1,ц) и у = уьЦ.ц). Построение сетки внутри области может быть рассмотрено в виде следующей краевой задачи: по заданным на dR х = хь{1,г]) и у = = Уь{1.Ц) (рис. 13.2) определить х = л:(,11) uy = y{l,y\) внутри области Ry ограниченной границей dR. Поскольку внутренние точки в расчетной области образуют регулярную сетку и границы совпадают с координатными линиями, определение хЦ.ц), уЦуЦ) упрощается по сравнению с решением задачи в физической области. Это особенно важно, если Рис. 13.2. Построение сетки как граничная задача в расчетной области. решение х(, т]), у (1,11) находится в результате решения уравнения в частных производных (см. п. 13.2.6). В определенной выше краевой задаче граничные условия являются условиями Дирихле. Однако часто имеет смысл ввести в рассмотрение граничные условия Неймана. Например, они ыли бы пригодными, если бы требовалось, чтобы координатные линии пересекали физическую границу по нормали. Это означает, что на определенных сегментах границы угол пересечения (обычно 90 ) координатных линий с границей задан и положение точек пересечения координатных линий с границей определяется в результате решения краевой задачи. Естественным обобщением является использование смешанных граничных условий там, где необходимо осуществлять контроль как положения точек на границе, так и ортогональности сетки на границе. При решении граничной задачи для определения положения внутренних точек сетки используются два широко развитых подхода. Один состоит в решении уравнений в частных производных (§ 13.2), второй - в интерполяции внутренних точек по граничным (§ 13.3). Прежде чем перейти к рассмотрению конкретных методов, будут рассмотрены типичные топологические соответствия между физической и расчетной областями (§ 13.1). При определении соответствия между точками физической и расчетной областей, т. е. х = х{1,ц) и (/= т]), необходимо, чтобы это было взаимно однозначное соответствие. Недопустимо, чтобы одна и та же точка физической плоскости отображалась в две точки расчетной области и наоборот. Это эквивалентно требованию, чтобы координатные линии одного семейства не пересекались, а координатные линии различных семейств пересекались лишь один раз. После установления соответствия х = х{1,ц) и у = 1/(1, л) его взаимная однозначность может быть определена из оценки детерминанта якобиана преобразования J отображение было взаимно однозначным, . печным и ненулевым. В зависимости от того, каким образом была построена сетка, для проверки взаимной однозначности величина J в каждой точке может быть определена либо аналитически, либо численно (§ 12.2). Подобная проверка может быть легко оформлена в виде компьютерной программы, которая быстро определит точки, где отображение неоднозначно. из (12.3). Чтобы I должен быть ко- § 13.1. Физические аспекты В данном параграфе будут рассмотрены типичные отображения границ одно- и многосвязных областей. Конкретный выбор из массы возможных отображений границ может существенно повлиять на деформацию сетки внутри области. 13J.L Односвязные области Односвязная область характеризуется тем, что любой замкнутый контур, лежащий внутри нее, может быть стянут в точку, не лежащую на границе области. При наиболее простом отображении область, определенная четырьмя кривыми, преобразуется в расчетной области к прямоугольному виду. Подобное отображение изображено на рис. 12.2. Если физическая область имеет некоторую специальную форму, то иногда имеет смысл сохранить эту форму и в расчетной области. На рис. 13.3, например, показано, как криволинейная физическая область L-образной формы может быть преобразована к прямоугольной L-образной расчетной области. Из рисунка видны основные преимущества такого преобразования. При при- ближенном сохранении формы области проще избежать сильной деформации (т. е. неортогональности (12.18)) сетки. Та же самая область L-образной формы в физической области может быть преобразована к прямоугольному виду в расчетной области (рис. 13.4). Теперь, однако, точки А и D излома 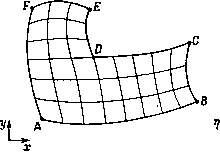 Рис. 13.3. Преобразование L-образной области с сохранением формы. образующей в физической области лежат на линии постоянного значения ц (точки А и в расчетной области. Построение численного алгоритма в области, изображенной на рис. 13.4, оказывается проще, чем в области, приведенной на 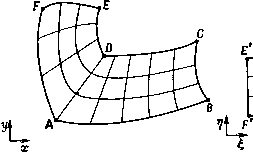 Рис. 13.4. Преобразование L-образной области в прямоугольник. рис. 13.3. Однако более сильная деформация сетки в физической области вблизи точек А и D может привести к большей потере точности, чем для сетки на рис. 13.3. Обратная ситуация возникает, если угловые точки расчетной области лежат на гладких участках границы (рис. 13.5) в физической области. Очевидно, что в этом случае сетка вблизи точек Л, и т. д. в физической области сильно искривлена, и здесь можно ожидать локальной потери точности решения. Кроме
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |