где V- (pv)=divpv. Поскольку (11.8) справедливо для любого V, подынтегральное выражение должно быть равно нулю:

+ V-(pv) = 0.

(11.9)

Данное уравнение называется уравнением сохранения массы

или уравнением неразрывно-у=(ц,1;,ш) сти. В декартовой системе координат (II.9) имеет вид

Объем V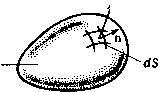

Рис. 11.2. Сохранение массы.

+ (Р) = 0. (11.10)

Удобно сгруппировать все члены, содержащие плотность, и записать (11.10) в виде

Р Idt или

dzi 1 гор

ди , -ду , dw

дг ]

9 iDt i

-f = 0.

= 0, (11.11)

(11.12)

Здесь D/Dt называется полной или конвективной производной по времени а S) - дилатацией. Для течений с постоянной плотностью (так называемых несжимаемых течений) уравнение (11.12) сводится к виду

= V-Vi

ди , dv . dw

дх ду дг

как для стационарных, так и для нестационарных течений.

(11.13)

11,2.2, Уравнение количества движения: невязкое течение

В соответствии со вторым законом Ньютона скорость изменения количества движения равна сумме действующих сил. Для малого элемента жидкости, рассматриваемого как замкнутая система (т. е. отсутствует поток через границы), второй закон Ньютона может быть записан в виде

(11.14)

где нижний индекс cs означает замкнутую систему.

Для неподвижного объема У, в котором возможно течение через границы (рис. 11.3), имеется следующая связь с замкнутой системой [Streeter, Wylie, 1979]:

5 pv rfKcs = J -jf (pv) + 5 pv (V . n) dS. (11.15)

Здесь pv -количество движения, v-n - проекция скорости на нормаль к поверхности контрольного объема. По теореме Гаусса

Объем V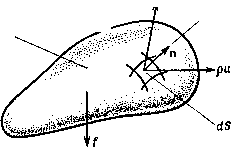

Рис. 11.3. Геометрия контрольного объема для уравнений Эйлера, соотношение (11.15) преобразуется к виду

JL J pydVcs=\ [i-(Pv) +V (pw)]dK. (11.16a)

Преобразуя производные в (11.16а) и используя (11.9), можно получить

(11.16Ь)

JpvdKes=SpdF,

где D\/Dt = d\/dt vv. Величина D\/Dt есть полная производная по времени от v (ускорение).

Таким образом, уравнение (11.14) принимает вид

(11.17)

т. е. произведение массы на ускорение равно силе.

Сумма в правой части (11.17) складывается из сил, действующих на поверхность контрольного объема (поверхностные силы), и сил, действующих на каждый его элемент (объемные или массовые силы). Наиболее распространенной массовой силой (и только она здесь рассматривается) является

Гравитационная сила тяжести. Природа поверхностных сил зависит от того, учитывается ли вязкость жидкости. Сначала будет рассмотрена невязкая жидкость. В этом случае поверхностные силы обусловлены лишь давлением, которое действует по нормали к поверхности. Тогда правая часть (11.17) может быть записана в виде

JF = 5pfdK- J pndS, (11.18)

где f - объемная сила на единицу массы. По теореме Гаусса правая часть (11.18) может быть преобразована к интегралу по объему

5]F = 5(pf-Vp)dK. (11.19)

Подстановка этого выражения в (11.17) дает

S[p--pf + Vp]dK=0.

(11.20)

Итак, для произвольного объема V

(11.21a)

Другая (консервативная) форма этого уравнения может быть получена из (11.16):

(pv) + V (pv V) = pf - Vp.

(11.2Ib)

Уравнения (11.21) называются уравнениями Эйлера и применимы, строго говоря, лишь для описания течений невязкой жидкости. Однако для многих течений влияние вязкости чрезвычайно мало и уравнения (11.21) являются весьма точным приближением.

Если массовая сила является силой тяжести, направленной в отрицательном направлении оси г, то уравнения Эйлера (11.21) в декартовой системе координат имеют вид

(11.22) (11.23) (11.24)

Уравнения (11.21) - (11.24) применимы для описания как сжимаемых, так и несжимаемых течений.