k - /-1, Г Л/. + , - Л/, k-l

(12.30)

В общем случае при преобразовании к обобщенным координатам уравнений второго порядка (п. 12.3.2) необходимо опреде-

наименьшее число дополнительных членов и, следовательно, позволяют разработать более экономный алгоритм расчета. В случае трех пространственных переменных построение полностью конформных или ортогональных стенок обычно невозможно. Поэтому уравнения должны быть записаны в обобщенных координатах, хотя и возможны некоторые упрощения по отдельным координатным направлениям или в локальных расчетных подобластях.

§ 12.2. Аппроксимация параметров преобразования

Если возможно аналитическое отображение физической области (х,у) в расчетную (g,л) что имеет место при простых конформных преобразованиях, параметры преобразования и т. д, могут быть определены точно. Обычно отображение определяется лишь для точек сетки, и параметры преобразования приходится определять численно. Для простоты в данном параграфе это будет проиллюстрировано в двумерном случае. Обобщение на трехмерные сетки проводится очевидным образом.

Дискретизация уравнений в обобщенных координатах проводится в области (g, л) и отображение обычно производится таким образом, что в области (g, т]) определяется однородная прямоугольная сетка (рис. 12.2).

Численное определение параметров преобразования может быть проведено обычными методами дискретизации (гл. 3 и 5). В п. 12.2.1 используются формулы с центральными разностями. Аппроксимация на основе метода конечных элементов описана в п. 12.2.2. Томпсон и др. [Thompson et al., 1985] предложили аппроксимацию на основе метода конечного объема. Однако для аппроксимации параметров преобразования и производных в рассматриваемых уравнениях рекомендуется использовать одну и ту же дискретизацию.

12,2.1, Формулы с центральными разностями

Аппроксимацию параметров преобразования удобнее всего провести через переменные х, х и т. д. Для точки Р (рис. 12.4) можно записать формулы с центральными разностями

ЛИТЬ некоторые вторые производные. Например,

ХЦ--д2- .

i, k-i ~ j, k + i, + 1

Здесь подразумевается, что сетка в плоскости {1,ц) равномерная, т. е. А = - ii = li - и т. д. Аналогично можно определить параметры у и т. д.

После определения основных параметров преобразования с помощью (12.30) и (12.31) обратные параметры 1х и т. д.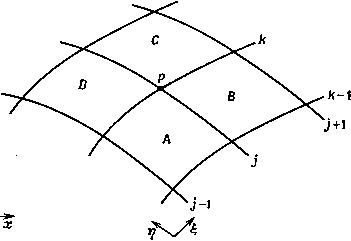

Рис. 12.4. Расчетная сетка в физической области.

можно получить из уравнений (12.7). Типичные уравнения движения жидкости (п. 12.3.3) можно записать более компактно с помощью членов типа появляющихся в них явно. Вторые производные обратных параметров, например Ixx, можно выразить через соотношения (12.31). Конкретный вид этих соотношений представлен выражением (12.81). После аппроксимации параметров xi и т. д. параметры сетки gu а, AR и 6 могут быть получены соответственно из уравнений (12.12), (12.15) - (12.17).

Аппроксимация параметров преобразования производится по формулам более высокого порядка, чем (12.30) и (12.31). Как правило, для дискретизации параметров преобразования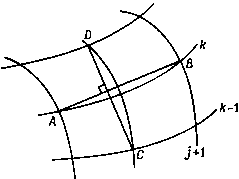

J-1 J

Рис. 12.5. Дискретная ортогональность.

тензора, могут быть отброшены. В случае двумерной ортогональной сетки 12 = 1 + 111 = 0. Если параметры преобразования и т. д. аппроксимируются численно, чрезвычайна важно, чтобы дискретное представление соответствующих членов gij было равно нулю. Так, например, для двумерной ортогональной сетки аппроксимация gi2 может быть осуществлена следующим образом:

g\2 = (/+1, k /-1, k) (/, k+\ ~ k-\) +

+ (У/4-i, k - k) (У/, k+i - У/, k-i) = 0. (12.32)

Геометрическая интерпретация выражения (12.32) представлена на рис. 12.5. Чтобы условие ортогональности выполнялось на дискретном уровне, необходимо чтобы линии АВ и CD были перпендикулярны. Следовательно, если параметры преобразования на ортогональной сетке определяются численно, сетка должна быть построена так (п. 13.2.4), чтобы выполнялись дискретные условия ортогональности.

12.2,2. Аппроксимация методом конечных элементов

При аппроксимации параметров преобразования методом конечных элементов также получаются уравнения (12.30) и (12.31). При изопараметрическом построении (п. 5.5.3) на четырех прилежащих элементах (Л, В, С и D на рис. 12.4) с били-

используются те же разностные формулы, что и для аппроксимации производных в уравнениях. Данный аспект будет рассмотрен в п. 12.2.3.

Если уравнения решаются на ортогональной сетке, члены пропорциональные внедиагональным элементам gi} метрического