

 |
 |
Разделы сайта
Читаемое
Обновления Jul-2025
|
Промышленность Ижоры --> Динамика жидкости: уравнения СИЯ. Принимается, что справедливы уравнения, подобные уравнению (11.1), однако термодинамические параметры являются функциями координат и времени, т. е. р = p{x,y,z,t), р = = р(х, Уу Zy t)y T = T(x,y,zJ). Кроме того, необходимо дать однозначное описание движения. В настоящей книге используется 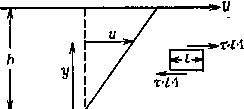 чХч\\\\\\\\\\\\ Плоский поток Рис. 11.1. Плоский поток, параллельный неподвижной поверхности. эйлеров подход, в соответствии с которым скорость и термодинамические параметры рассматриваются в фиксированных точках (х, Уу г, t) пространственно-временного объема. В противоположность этому подходу при лагранжевом описании исследуются отдельные частицы жидкости, положение и термодинамические свойства которых считаются зависимыми переменными. Связь между подходами Эйлера и Лагранжа обсуждается в работе фон Швинда [von Schwind, 1980]. Наличие в движущейся жидкости сдвиговых сил приводит к понятию динамической вязкости. Рассмотрим плоскость, движущуюся со скоростью и параллельно другой неподвижной плоскости (рис. 11.1). Жидкость, прилегающая к верхней пластине, удерживается у ее поверхности (т. е. движется со скоростью U) силой тЛ, где Л -площадь пластины, т -сдвиговое напряжение. На элемент жидкости, расположенный между пластинами, действуют две сдвиговые силы (т-/-1). На верхней поверхности элемента эта сила направлена вправо, на нижней - влево. Жидкость, прилегающая к нижней пластине, удерживается у ее поверхности под действием силы тЛ. Экспериментально обнаружено, что сдвиговое напряжение прямо пропорционально градиенту скорости ди/ду, т. е. г = 11 ди/ду.. (11.3) Коэффициент пропорциональности pi называется вязкостью (динамической). Вязкость измеряется в кг/м-с. Для рассмотренного примера сдвиговое напряжение т постоянно и, следовательно, 9Ср распределение скорости описывается соотношением u/U = y/h. (11.4) Уравнение (11.3) описывает поведение так называемых ньютоновских жидкостей. Течения воздуха или воды подчиняются закону (11.3). Неньютоновские жидкости, т. е. жидкости, для которых не выполняется условие (11.3), описаны Тэннером [Tanner, 1985]. Вязкость газов, подобных воздуху, при нормальных температуре и давлении с высокой точностью зависит лишь от температуры. Для воздуха вязкость увеличивается с температурой по закону (Г - абсолютная температура). Типичные значения вязкости приведены в табл. 11.1. Для жидкостей, подобных воде, вязкость слабо зависит от давления, но сильно изменяется с температурой. В отличие от газов вязкость жидкостей, как правило, быстро падает с увеличением температуры. Характерные величины вязкости приведены в табл. 11.2. Для течений, сопровождающихся изменениями температуры, справедлив закон Фурье, согласно которому локальная скорость переноса тепла прямо пропорциональна локальному градиенту температуры, т. е. Qi = -k> (11.5) где - скорость переноса тепла на единицу площади в направлении Xi, а k - теплопроводность. Следует отметить аналогию между соотношениями (11.3) и (11.5). Если значения температуры пластин на рис. 11.1 различны, то в соответствии с законом (11.5) в жидкости будет иметь место перенос тепла, определяемый соотношением Qy=-k. (11.6) Теплопроводность измеряется в Вт/м-К. Подобно вязкости теплопроводность газов увеличивается с температурой. Для жидкостей, например для воды, теплопроводность слабо увеличивается в диапазоне температур от 0° до 100 °С при давлении в одну атмосферу. Типичные величины теплопроводности воздуха и воды приведены в табл. 11.1 и 11.2. Вязкость и теплопроводность входят в рассматриваемые в дальнейшем уравнения импульса и энергии (см. (11.31) и (11.38)). Удобно ввести в рассмотрение кинематическую вязкость V и тепловую диффузию а, определяемые соотношениями li k v = и а = где Ср -удельная теплоемкость при постоянном давлении. Значения V и а измеряются в м/с и определяют диффузию соответственно количества движения и тепла. Для газов, подобных воздуху, V и а увеличиваются с температурой (табл. 11.1). В жидкостях кинематическая вязкость v быстро падает с увеличением температуры, а тепловая диффузия а увеличивается незначительно (табл. 11.2). Более подробно свойства жидкостей и связь этих свойств со свойствами молекул описаны Лайтхиллом [Lighthill, 1963] и Бэтчелором [Batchelor, 1967].Свойства наиболее распространенных жидкостей приведены в работе [Eckert, Drake, 1972]. § 11.2. Уравнения движения Для вывода уравнений движения жидкости обычно рассматривается малый контрольный объем и требуется, чтобы для жидкости, протекающей через этот объем, выполнялись законы сохранения массы и энергии, а скорость изменения трех компонент импульса была бы равна соответствующим компонентам приложенных сил. Это позволяет получить пять уравнений, которые в комбинации с уравнением состояния позволяют определить шесть величин: обычно это значения р, р, Г, и, у, ш. В потоках, связанных с процессами горения, а также в некоторых геофизических течениях фигурирует более одной компоненты жидкости. Для каждой новой компоненты необходимо дополнительное уравнение (сохранение компоненты). Наоборот, для некоторых течений достаточно рассматривать не все из шести переменных и для описания таких течений требуется меньшее число уравнений. 1L2J. Уравнение неразрывности Согласно закону сохранения вещества, для произвольного неподвижного объема V (рис. 11.2) скорость изменения массы внутри него равна потоку массы через поверхность 5, ограничивающей объем V, т. е. 4r\9dV=\9WndS. (11.7) где п - единичный вектор нормали (внешней). По теореме Гаусса [Gustafson, 1980] поверхностный интеграл может быть заменен на объемный. Уравнение (11.7) принимает вид S[ + V.(pv)]dK=0, (11.8)
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |