(18.170)

В? = 0.5р(А/+1~Еж/2) ,

F/+1/2 = 0.5 (Р/ + Ру+1 - Та, /+1/2Ф/+1/2). (18.171)

Член Ф/+1/2 эквивалентен второму члену в правой части уравнения (18.162) и состоит из вкладов /+1/2 отдельных (/-х) характеристик

/-м/2 = Ял./+1/2 [l - Ч)]/+1/2Тл +1/2(я/+1 -q/). (18.172)

В формулах (18.170) Е определяется выражением

Е/±1/2 = [ТлЙТл]у,/2, (18.173)

diagQy:fci/2 = {i(l -Чг)}у,/2. (18.174)

Уравнение (18.169) блочно-трехдиагональное, и для его решения применим алгоритм, описанный в п. 6.2.5. Если выражение (18.171) подставить в (18.169), то пространственную дискретизацию можно трактовать как центрально-разностную для потока F плюс дополнительная численная диссипация, составленная из отдельных характеристических переменных.

Путем введения приближенной факторизации (см. п. 18.3.2) данный алгоритм практически без изменений может быть обращен на многомерный случай. В работе [Yee, 1987] обсуждается возможность диагонализации левой части уравнения (18.169), в результате чего стационарное решение может быть получено более экономным образом.

Для течений в нерегулярной расчетной области описанный алгоритм может быть реализован в обобщенных координатах {Yee, Harten, 1985]. В результате получается алгоритм, аналогичный описанному в п. 18.4.1, в котором диссипативные добавки к конвективным членам строятся по схеме TVD. По описанному алгоритму Ии (Yee) на сетке 163 X 49 рассчитал стационарное невязкое течение у профиля NACA-0012, расположенного под углом атаки 7°, при Мех. = 1.2. Было проведено сравнение с расчетом по алгоритму ARC2D [Pulliam, Steger, 1985], по существу совпадающему с алгоритмом, описанным в п. 18.4.1. Как и следовало ожидать, описанный алгоритм дает лучшее решение в окрестности головного скачка и возникающего на верхней поверхности профиля хвостового скачка. Отличие результатов, полученных двумя методами, становится больше при

увеличении числа Маха набегающего потока до Мсх.= 1.8. Отличие возникает непосредственно вблизи скачков и обусловлено локальным увеличением их интенсивности.

Вдали от скачков оба метода дают практически совпадающие решения; в частности, распределение давления по поверхности оказывается одинаковым. Следует заметить, что определение численной диссипации в соответствии со схемой TVD, даже если оно проводится лишь в правой части уравнения (18.169), значительно увеличивает время счета.

Для нестационарных течений более точные результаты по-.лучаются по явной схеме, т. е. при р = О в уравнениях (18.169) -(18.174). В работе [Yee, 1986] рассмотрена дифракция плоского скачка на профиле NACA-0018, расположенного под углом атаки 30°. Скорость скачка Ms =1.5, решение получено на С-сетке размером 299X79. На рис. 18.13 приведено сравнение с экспериментальными интерферограммами плотности из работы [Mandella, Bershader, 1987]. Очевидно хорошее совпадение с экспериментальными данными.

Можно отметить, что интерпретация схем TVD как алгоритмов введения дополнительной численной диссипации в центрально-разностную аппроксимацию невязких потоков позволяет -легко модифицировать существующие алгоритмы [Yee, 1987]. Для осуществления этой модификации необходимо рассмотреть локальные градиенты, и если эти градиенты оказываются большими, т. е. вблизи скачков, вводить TVD-диссипацию.

Дискретизация TVD невязких членов легко комбинируется с центрально-разностной аппроксимацией вязких и турбулентных членов в уравнениях Навье-Стокса. В результате получаются алгоритмы, аналогичные (18.169), с блочно-трехдиаго-нальными матрицами. Решение многомерных сжимаемых уравнений Навье-Стокса методом установления с аппроксимацией TVD может быть получено при помощи приближенной факторизации [Yee, 1987], блочной бидиагонализации [Lombard et al., 1986] или по схеме релаксации [Chakravarthy, 1987].

Кроме того, алгоритмы TVD могут быть построены на основе расщепления вектора потока, подобного рассмотренному в п. 14.2.5. В работе [Walters et al., 1986] описан алгоритм, в котором методом установления решаются сжимаемые уравнения Навье-Стокса. В алгоритме используется расщепление вектора потока [van Leer, 1982] в сочетании с приближенной факторизацией или релаксацией. Схему расщепления потока также можно интерпретировать [MacCormack, 1984] как модификацию численной диссипации в центрально-разностной аппроксимации левязких потоков.

Интерферограммы Лскрттнный скачок

Плоский скачок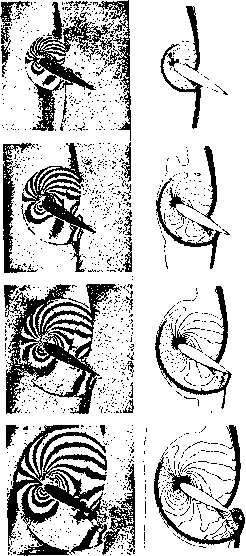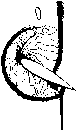

Симметричная схема TVD 2 го порвдка

Рис 18 13 Профили плотности при прохождении ударной волны профиля NACA-0018 при угле атаки 30° [Yee, 1986J.