Для течения около несимметричной задней кромки (рис. 18.9) применение обобщенных координат позволяет построить расчетную область, в которой задняя кромка конечной толщины превращается в плоскую пластину нулевой толщины, т. е. в расчетной области точка D совпадает с точкой В.

Решение по описанному выше алгоритму было получено [Srinivas, Fletcher, 1986] при Мех, = 0.4 и Re = 26 X Турбулентные эффекты учитывались при помощи алгебраической

Е F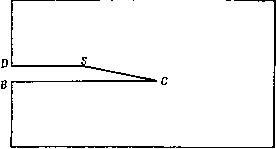

Рис. 18.9. Асимметричная задняя кромка; течение слева направо.

модели турбулентной вязкости (18.12) -(18.16). Алгоритм использовался как метод установления для определения стационарного решения. Для распределения скоростей вблизи и за задней кромкой сходимость считалась достигнутой, если среднеквадратичное значение (RHS) в (18.148) становилось меньше 10-. На сетке 41(х, g) на 82 ((/,т]) для этого понадобилось около 1000 шагов по времени.

На твердой поверхности DSCB обе компоненты скорости полагались равными нулю. Вблизи твердой поверхности для определения изменения нормальной и тангенциальной компонент скорости использовались пристенные функции (п. 18.1.1). На входной поверхности {АВ м ED на рис. 18.9) вдали от тела и=\Л и у = 0. Вблизи тела использовался степенной профиль с показателем 1/7 в соответствии с локальными числами Рейнольдса. Давление на входной поверхности определялось через решение во внутренней области при помощи дискретного представления характеристического соотношения

(18.150)

На свободных границах AG и EF\ u=\.Q, v = 0. Давление определялось через решение внутри области из дискретного

Представления характеристического соотношения

ду ду

На выходной границе {FG на рис. 18.9)

-=0 -=0

дх дх

-pa- + 0.3(p-pJ = 0.

(18.151)

(18.152)

Уравнение (18.152) является граничным условием без отражений, что способствует ускорению сходимости к стационарному состоянию (п. 14.2.8).

В результатах, представленных на рис. 18.10, х измеряется от задней кромки (точка С на рис. 18.9). Численные результаты.

D О данный расчет

Ж эксперимент (Cleary et а1 , 1980 --расчет (Cleary et 01 , 1980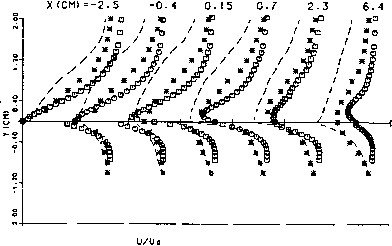

li 5 3 3 3 V Г.о

Рис. 18.10. Распределение скорости за задней кромкой, полученные на сетке 41 (х) на 82(у), хорошо согласуются с экс-

периментальными данными зультаты [Cleary et al., 1980

Cleary et al., 1980]. Численные pe-получены конечно-разностным ме-

тодом при помощи модели турбулентности, основанной на двух

уравнениях, на сетке 60(х) на 100(у). Однако более позднее конечно-разностное решение [Horstman, 1983] на сетке 79 на 82 с модифицированной моделью турбулентности лучше совпадает с экспериментальными данными.

§ 18.5. Численная диссипация

В § 9.2 ошибка аппрокситугации, возникаюпхая при замене континуальных уравнений разностными, рассматривалась как источник численной диссипации и дисперсии. Было показано, что и то, и другое нежелательны. Особенно вредна численная диссипация, если она становится по величине сравнимой или даже больше физической диссипации.

Однако в § 9.2 также отмечено, что диссипация, численная или физическая, приводит к быстрому затуханию коротких волн и гораздо слабее влияет на длинные волны. Данное свойство позволяет использовать численную диссипацию при расчетах течений с большими числами Рейнольдса или с ударными волнами.

При исследовании поведения течения часто полезно провести разложение Фурье для физических переменных, например компонент скорости или давления, приписав им амплитуды, связанные с различными волновыми числами. Разложение Фурье может быть проведено в зависимости от конкретного случая по времени или пространству. Волновое число можно интерпретировать как величину, обратную масштабу времени или длины.

Мгновенное распределение скорости при переходе через скачок, полученное, например, из решения уравнений Эйлера, приведено на рис. 18.11(a). Фурье-представление и(х) можно записать в виде

и{х)= Z aexp{imx\ (18.153)

где т - волновое число (§ 9.2), ащ - амплитуда т-й компоненты. Результат соответствующего спектрального анализа, т. е. зависимость амплитуды от волнового числа, приведен на рис. 18.11(b). Очевидно, что большие амплитуды соответствуют малым волновым числам, т. е. большим масштабам длины. Малые, но конечные амплитуды связаны с большими волновыми числами, т. е. малыми масштабами длины. Легко видеть, что в представлении разрывного распределения скорости, образованного ударной волной, имеются все масштабы.

Решения, полученные на конечной сетке, могут представлять лишь конечное число членов дискретного ряда Фурье (18.153). На сетке с NX равномерно распределенными точками в реше-