

 |
 |
Разделы сайта
Читаемое
Обновления Aug-2025
|
Промышленность Ижоры --> Динамика жидкости: уравнения устойчивости: (2ji/Re р) [2у/Рг + (2/3)0-5] + [ + + (2)0.5] д (18.41) где а - скорость звука. Из вида условий устойчивости (18.40) и (18.41) следует, что в трехмерном случае ограничение на шаг по времени более жесткое, чем в двумерном и одномерном случаях. Чтобы избежать этого ограничения, Мак-Кормак [MacCormack, 1971] в описанную выше схему ввел расщепление по времени. Расщепление по времени, аналогично описанной в § 8.5 процедуре, приводит к последовательности одномерных пространственных операторов. Для уравнения (18.6) одномерные операторы могут быть представлены в виде 4i% = P.(K)%k (18-42) Здесь уравнение (18.42) эквивалентно уравнениям Ч/. ft = ЧЬ - k - k] ч;%=0.5 (q;., + q;.,) - 0.5 [f;. , - f; Аналогичные выражения для (18.43) могут быть получены из уравнений (18.35) и (18.36). Весь алгоритм определения решения на новом временном слое вместо (18.35), (18.36) принимает вид Симметричная картина повторяющихся пространствных операторов от At/2 необходима, чтобы получить алгоритм второго порядка по времени. Устойчивость алгоритма (18.44) определяется устойчивостью отдельных операторов. Таким образом, аналогичное (18.41) ограничение на Рх при произвольных Дл: и Ау имеет вид (ji/Re р) [2у/Рг + (2/3) -5 {x/y)] + l\u\ + a]x Очевидно, что возможно применять большие шаги по времени. Дополнительное преимущество состоит в том, что для различных координатных направлений могут быть использованы различные шаги по времени. Для обтекания тонких тел, параллельных оси л:, необходимы малые в направлении у шаги сетки для разрешения больших пространственных градиентов скорости и тем- пературы, связанных с поверхностным пограничным слоем. Применение схемы расщепления по времени (18.44) позволяет избежать влияния на Atx ограничения на шаг Aty. Схема расщепления по времени эффективна, хотя и требует введения вспомогательных процедур вблизи границ [Peyret, Taylor, 1983]. Схема Мак-Кормака в сочетании с методом установления (п. 6.2.4) малоэффективна для определения стационарного решения, если только не применяется многосеточный подход (п. 6.3.5) [Chima, Johnson, 1985]. 18.2,2, Схема Рунге - Кутты В явной схеме Мак-Кормака, описанной в п. 18.2.1, второй порядок точности по пространству достигается весьма экономным образом. Однако ограничение на шаг по времени (18.45) существенно снижает общую эффективность алгоритма при нахождении стационарного решения методом установления для течений с большими числами Рейнольдса. Из условия (18.45) следует, что при больших числах Рейнольдса условие устойчивости схемы расщепления Мак-Кормака эквивалентно тому, что число Куранта С = (\и\-\-а)А1х/1!1 не превышает единицу. Конечно, влияние больших чисел Рейнольдса непосредственно сказывается и в ограничении на шаг по пространственной переменной для правильного разрешения тонкого пограничного слоя. В результате применения метода прямых (§ 7.4) из исходной системы уравнений можно получить систему обыкновенных дифференциальных по времени уравнений. Для ее решения удобно использовать маршевые по времени схемы Рунге-Кутты, поскольку для этих схем можно использовать большие, чем в схеме Мак-Кормака, значения числа Куранта. Например, для нестационарных течений можно использовать схему Рунге-Кутты четвертого порядка (7.53). Эта схема при достаточно малых диссипативных членах устойчива, если С < 2 V2. Для нахождения стационарных решений методом установления имеет смысл использовать рациональную схему Рунге- Кутты (РРК) [Wambecq, 1978] первого или второго порядков поскольку она позволяет использовать еще большие числа Куранта. Рациональная схема Рунге-Кутты будет продемонстрирована на уравнении общего вида dqldt = W{q), (18.46) Это уравнение можно рассматривать как одну из компонент системы (18.6) после проведения пространственной дискретизации. Схема РРК использовалась в работе [Satofuka et al., 1986]. Для дискретизации первых и вторых пространственных производных в уравнениях (18.6) -(18.10) рекомендуется использовать обычные трехточечные центральные разности. -1.2 -0.8- NACA65(12)10 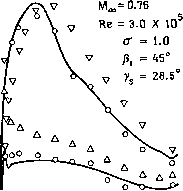 данное решение, Pj/Pi = 1 229 Д V эксперимент без отсоса на конце стенки О эксперимент с отсосом на конце стенки Хорда Рис. 18.3. Сравнение с экспериментальным распределением давления в каскаде 65(12)10 ([Satofuka, 1986]; печатается с разрешения AIAA). Двухшаговая схема РРК применительно к уравнению (18.46) может быть построена следующим образом. Промежуточные поправки определяются выражениями Ад = AtW {q% Aq = AtW ( + с Aq% Aq = {\-b)Aq + bAq\ и решение на новом временном слое - по формуле в уравнении (18.47) (е, f) означает скалярное произведение, т.е. (е, \)-=Y,edi,
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |