Для определения решения уравнение (17.56) разбивается на две части. Предварительная оценка значений и + получается в результате определения и* из уравнения

U* + Дг V (u u*) - (-) Vu* = u - MS/p . (17.57> На второй стадии

u +i = u*-Д/убр + (17.58)

Из условия удовлетворения и + уравнению неразрывности следует

V . u+i = о = V U* - у2бр +

у2б/7+1 = (1/Д0У- U*. (17.59>

Очевидно, что (17.59)-уравнение Пуассона для поправки к. давлению. Это уравнение эквивалентно уравнению (17.24) в методе проекций, отличие заключается лишь в величине и*.

Однако существует иной способ определения u + удовлетворяющего уравнению неразрывности. К скорости и* можно добавить безвихревую добавку обеспечивающую выполнение закона неразрывности, т. е.

V . u +i = V U* -f V = 0. (17.60>

Поскольку скорость безвихревая, можно ввести потенциал так, что = V. Уравнение (17.60) принимает вид

у2</ = -уи*. (17.61)

Уравнение (17.61) есть уравнение Пуассона для эквивалентное (17.59). Если используются эквивалентные граничные условия, то

6р+ = ф/М, (17.62)

Таким образом, если в результате решения уравнения (17.61) определены значения ф, то непосредственно находится из уравнения (17.62). Граничные условия для (17.61) обычно определяют значения дф/дп, подчиняющиеся глобальному ограничению, эквивалентному (17.4),

5 -rf5= 5 уЛ = - 5 V u*rfA (17.63)

На практике дф/дп полагается равным нулю на твердой поверхности, но на открытых границах эти значения выбираются так чтобы удовлетворялось условие (17.63). Решение для ф не обязательно будет удовлетворять условию /5 = О на границе. Поэтому рекомендуется при решении (17.57) использовать для

s = -

Условие (17.64) с точностью до О (At) обеспечивает выполнение равенства и+=0, где s - направление касательной к границе. Таким образом, на (п--1)-м временном слое обеспечивается выполнение условия прилипания.

Для нестационарных задач уравнение (17.61) необходимо решать на каждом шаге по времени. Однако для стационарных несжимаемых течений более эффективно заменить (17.61) уравнением

V2</, + vu* = 0, (17.65)

которое решается маршевым по времени методом совместно с уравнением (17.57). Обычно для решения (17.65) используется больший шаг по времени или же оно решается после того, как сделано три или четыре шага по времени для уравнения (17.57). Для малых времен уравнение (17.61) будет выполняться лишь приближенно. Поэтому в давление необходимо ввести нижнерелаксационную поправку, т. е. заменить (17.62) на

pn+i = pnj (17.66)

Выделение в поле скоростей безвихревой составляющей, т. е. составляющей, которая может быть получена из потенциала скорости, как в (17.61), лежит в основе метода проекций Чо-рина [Chorin, 1967] (см. п. 17.1.4). Впервые вспомогательная потенциальная функция явно была использована в методе SMAC [Amsden, Harlow, 1970]. Позднее такой подход применялся в работах [Dodge, 1977; Cazalbonu et al., 1983; Kim, Moin, 1985], где использовалась конечно-разностная аппроксимация, и в работе [Ки et al., 1986b] в сочетании с псевдоспектральным методом. В работах [Briley, 1974; Ghia, Sokhey, 1977; Yashchin et al., 1984; Briley, McDonald, 1984] вспомогательный потенциал использовался для определения поля поперечных скоростей при моделировании течений в каналах (п. 16.2.2). В работе [Khos-1а, Rubin, 1983] применялась концептуально сходная идея расщепления скорости для расчета течений в вязких слоях большой толщины.

17,2.3. Метод SIMPLE

В данном семействе алгоритмов используется дискретизация уравнений по методу конечных объемов (§ 5.2) на разнесенных сетках (п. 17.1.1). Этот метод был предложен в работе

U* на твердой поверхности граничное условие

[дФ т

[Patankar, Spalding, 1972] и детально описан в работе [Patankar, 1980]. Аббревиатура SIMPLE происходит от Semi-Implicit Method for Pressure-Linked Equations и описывает итерацион-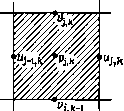

(а) Уравнение неразрывности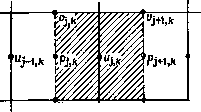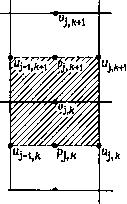

(b) Уравнение импульса no оси X (с) Уравнение импульса по оси /

Рис. 17.9. Контрольные объемы, используемые в методе SIMPLE.

ную процедуру решения дискретных уравнений. Итерационная процедура здесь рассматривается как метод установления для решения нестационарных уравнений (17.1) - (17.3) в дискретном виде с целью определения стационарного решения. Будет показана важная связь с методом вспомогательной потенциальной функции (п. 17.2.2).

На разнесенной сетке для различных уравнений используются различные контрольные объемы (рис. 17.9). Кроме того, сдвинуты сеточные индексы, связанные с определенными зависимыми переменными (рис. 17.9). В результате физическое положение значения p/+i/2, k совпадает с положением Uf, k, а р/, k-\-\/2 совпадает с vj, k- Приведенная ниже дискретизация соответст-