

 |
 |
Разделы сайта
Читаемое
Обновления Aug-2025
|
Промышленность Ижоры --> Динамика жидкости: уравнения HAY q =q?-2. k - U k + k - + U, Очевидно, что каждый шаг алгоритма приводит к блочно-трехдиагональным системам уравнений, для решения которых имеются эффективные численные методы (п. 6.2.5). Поскольку трапецеидальная разностная формула по времени нейтрально устойчива, в правую часть (17.51а) введен явный сглаживающий член четвертого порядка, подавляющий нелинейную неустойчивость. Неявный сглаживающий член второго порядка, введенный в левую часть (17.51), уравновешивает явное сглаживание во время нестационарного периода, препятствует снижению скорости сходимости к стационарному состоянию. Параметры ге и 8/ выбираются так, чтобы искусственная диссипация была пренебрежимо мала по сравнению с физической, которая в данном случае определяется величиной 1/Re. Использование искусственной диссипации обсуждается ниже в § 18.5. Для сложных геометрий имеет смысл использовать обобщенные координаты (гл. 12). Соответствующий алгоритм, аналогичный описываемому в § 18.4, использовался в работе [Steger, Kutler, 1977] для исследования вихревых следов и в работе [Kwak et al., 1986а] для расчета течений в трубопроводах двигателей. Как ИБП. 8.2.2, из (17.49) получается линейная относительно Aqn+\ система уравнений. Члены F + 0+ и q + разлагаются в ряд Тейлора в окрестности временного слоя п. В результате получается Следовательно, (17.49) можно записать в виде {l + 0.5 М [l.A + Lyb - (l + Lyy)]} Aq-+ = RHS, (17.50) RHS = М [(D/Re) (L + Lyy) - L,F - L,G]. Левая часть подвергается приближенной факторизации (см. п. 8.2.2) и решается в два этапа с добавлением искусственной диссипации: l + 0.5 At [lA - l ) + ti Axl, J Aq- = = rhs - [{VA.f + (VA q . (17.51) \ + 0.5 а/ (l,B - Lyy) + 8, AfLyy] Aq + = Aq*, где Re - число Рейнольдса, рассчитанное по турбулентной вязкости, а и xl - характерные расстояния, которые волны давления и завихренности проходят за заданный отрезок времени. Для течений в каналах Xl -общая длина канала, а 2% -расстояние между стенками канала. Например, для течения около кругового цилиндра при Re = 40 и А = 0.1 в работе [Kwak et al., 1986а] рекомендуется выбирать в диапазоне 0.1 < < 2 < 10. Из расчетов следует, что скорость сходимости не сильно зависит от а, если эта величина выбирается в указанном диапазоне. В работе [Kwak et al., 1986b] использовался указанный алгоритм для расчета вихревой пелены, образующейся при обтекании столба кругового сечения, стоящего на плоскости, несжи- Можно заметить, что искусственная скорость звука а присутствует в выражениях для А и В. Собственные числа А и В равны Xa = u, и, u±{a + uf\ Ib = v. v. v±(a + vf\ (17.52) Нестационарное решение можно разложить на отдельные моды вида ехр(-ЯлО и т. д. Таким образом, при больших значениях различные моды будут затухать с супхественно различными скоростями. В этом случае система уравнений (17.47) называется жесткой (§ 7.4). Если бы для маршевого по времени решения системы (17.47) использовался явный алгоритм, жесткость, связанная с большими значениями а, проявилась бы в виде сильного ограничения на А/, связанного с устойчивостью. Этого удается избежать при помощи неявного алгоритма (17.51). Однако в работе [Steger, Kutler, 1977] для сохранения первого порядка точности по времени уравнения (17.51) рекомендуется использовать условие а2< 1/А. (17.53) Если сделать слишком малой величиной, не будет достаточно точно выполняться уравнение неразрывности (17.1), что приведет к неустойчивости нестационарного решения. В работе [Kwak et al., 1986а] предложена следующая нижняя граница для а. Для ламинарных течений >[+Ш(У&)Т-. для турбулентных течений маемой жидкостью. Картина течения при числе Рейнольдса (рассчитанном по диаметру цилиндра), равном 1000, приведена на рис. 17.8. Траектории частиц, изображенные на рис. 17.8, получены на сетке, содержащей примерно 100 000 узлов. Для 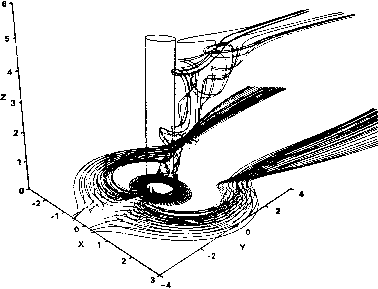 Рис. 17.8. Траектории частиц при обтекании цилиндра на плоскости, Re = = 1000 ([Kwak et al., 1986b]; печатается с разрешения NASA). достижения стационарного решения понадобилось около 800 итераций. Траектории частиц указывают на наличие сильной первичной вихревой структуры и на образование вторичных вихрей, которые переносятся по нормали к пластине (в сторону увеличивающихся значений г), прежде чем они сносятся основным потоком (в направлении увеличения у). 17.2,2. Вспомогательная потенциальная функция Данный метод описывается здесь в контексте метода установления (§ 6.4) к расчету стационарных решений. Удобно записать систему (17.1) - (17.3) в векторном виде. Дискретизация по времени позволяет записать уравнения импульса в виде д7 + V (u-u+O + VP + V 6/7-+ - () VV = О, (17.56) где -f 6+
|
|
© 2003 - 2025 Prom Izhora
При копировании текстов приветствуется обратная ссылка |