ными методами пограничного слоя [Cebeci, Bradshaw, 1977], предпочел проинтегрировать уравнения (16.211) и (16.212) по у, а для замыкания системы использовал эмпирические соотношения. В результате получился очень экономичный маршевый алгоритм для расчета вязкой области. Однако использование эмпирических соотношений предполагает, что внешние условия (угол атаки, геометрия тела и т. д.) должны подходить под класс течений, для которых эти соотношения имеют место. Напротив, прямое решение уравнений (16.211) - (16.216) ограничено лишь предположениями, сделанными при выводе укороченных уравнений Навье -Стокса, т. е. на пренебрежении осевой вязкой диффузией в уравнении (16.212) и всеми вязкими членами в (16.213).

В работе [Le Balleur et al., 1980] дефектное описание и интегральный вязкий метод использовались для установления следующей связи между вязкой и невязкой областями:

Л10 = Л2б- + Л. (16.217)

где © = {y/(i/2-f v)}y=o, значения А\, Лг, Лз и б* определяются текущими вязким и невязким решениями. Уравнение (16.217) является эквивалентным выражением (16.200). При прямом проходе, который пригоден для описания слабых взаимодействий, из уравнения (16.217) получается скорость инжекции v на поверхности тела, необходимая для расчета поправок к невязкому течению. При отрыве А\ обращается в нуль, что приводит к необходимости применять либо обратный (эквивалентный (16.202)), либо полуобратный (эквивалентный (16.203)) метод ,(рис. 16.29).

При прямом проходе (рис. 16.29) из предварительного значения угла поворота потока в*, полученного из (16.217), в ре-.зультате нижней релаксации получается значение 6+. Перед точкой отрыва и за ней используется полуобратный метод. Центральное место в этом методе занимает связь

- = flity-{t)) 06.218)

тде {dp/dxy и {dp/dx) - градиенты давления в текущих (обратных) вязком и невязком решениях. В работе [Le Balleur, 1981] для определения функциональной связи (16.218) в явном виде использовался анализ Фурье системы уравнений, из которых получено соотношение (16.217). В комбинации с релаксацией в = O-f (о(в* --в) весь полуобратный алгоритм может быть записан как

где р = (l - М), & = Л25*М1, 0<со<2, - поверхностное (невязкое) число Маха. Для локально сверхзвукового течения в работе [Le Balleur, 1981] предложена другая форма уравнения (16.219). Можно заметить, что хотя Ai в (16.217) в точке отрыва обращается в нуль, в уравнении (16.219) не возникает особенностей.

В работе [Le Balleur, 1981] дано подробное изложение описанного выше алгоритма, представлены результаты расчета течения у трансзвукового профиля под углом атаки с турбулентным отрывом. Отмечается очень хорошее совпадение с экспериментальными данными. По существу тот же подход может быть

0 х)

Нижняя релаксация

Рис. 16.29. Полуобратный метод.

использован для взаимодействия ударной волны с пограничным слоем [Le Balleur, 1984].

16,3.7. Вязко-невязкое взаимодействие с использованием уравнений Эйлера

Для течений, в которых можно ожидать появления сильных скачков, предпочтительнее в невязкой области решать уравнения Эйлера. В этом случае связь между перекрывающимися невязкой и вязкой областями должна быть рассмотрена более детально. В работе [Johnston, Sockol, 1979] разработан метод, основанный на дефектном описании взаимодействия, аналогичном (16.211) -(16.213). В этом методе стационарные двумерные уравнения Эйлера представляются в форме

дх ду

Компоненты векторов F и G приведены в (14.95).

(16.220)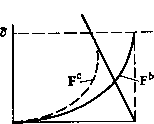

Рис. 16.30. Составная конструкция F.

перек вязкого слоя б и комбинации результатов получается следующее условие:

G=o=Gi;=o + -5(F-FOdy. (16.222)

предполагается, что в вязком слое решение уравнений Навье - Стокса аппроксимируется выражением F = F-+-F -Р=(> (рис. 16.30), где F* -решение, полученное на основе уравнений пограничного слоя или укороченных уравнений Навье - Стокса. В результате подстановки F и F в уравнение (16.222) получается

G=o = gUo + 5 (F=o - F) dy, (16.223)

На практике уравнение (16.223) используется как граничное условие для G{l), G(2) и О(4) при у = 0; 03) при у = 0 - давление на поверхности, которое определяется обычно из уравнения нормальной составляющей импульса. Можно заметить, что G(l) при у = 0 совпадает с инжектируемым (по нормали) импульсом и соответствующая компонента (16.223) эквивалентна (16.197). Дополнительные граничные условия G(2)y=o и т. д. необходимы, поскольку в невязкой области решаются уравнения Эйлера, а не трансзвуковое уравнение потенциала. В работе [Le Balleur, 1984] отмечается, что дополнитель-

Стационарные двумерные уравнения Навье -Стокса, описы* вающие течение в непосредственной близости от стенки, записываются в виде

+ = 0. 06.22

Компоненты векторов F* и в (16.221) приведены в п. 11.6.3. В результате интегрирования уравнений (16.220) и (16.221) по-